本篇目录:
...旋转平移后的坐标,怎么求旋转中心、角度和平移量
1、向量法:对于平面图形,可以设图形上任意一点为x,y,该点绕旋转中心旋转后的对应点为x’,y’,通过两点式求得图形上任意一点到旋转中心的距离以及该点到旋转中心的垂线与x轴夹角,从而求出旋转中心坐标。
2、绕着某个点旋转90度的坐标公式:r=(x1-n)+(y1-m)。在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。

3、旋转角度计算公式:C=(BX-AX,BY-AY)。旋转角度是一个重要的数学和几何概念,广泛应用于物理、工程、计算机图形学、机器人学等领域。
4、先用量角器下方的横线压住所要旋转图形的边,读出旋转角度,并在相应角度上方的纸面打上点。
平面向量加法(a+b)+c=a+(b+c)怎么作图证明
1、由A,B,C三点各向x轴引一条垂线,分别为AE,BF,CG,这三边长度分别为上述三向量的纵坐标,而OE,OF,OG分别为上述三向量的横坐标。
2、a+0=0+a=a。向量加法的运算律:交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)。

3、需要注意的是,向量加法具有交换律和结合律。也就是说,任意两个向量的加法可以交换顺序,多个向量的加法可以改变括号结合的顺序,而得到的结果是一样的。
4、平面向量运算法则是指平面上两个向量之间的加法和乘法运算规则。平面向量在二维平面上具有大小和方向,并可以进行各种运算。向量的加法是将两个向量的对应分量相加得到新的向量。
5、向量积几何意义是以a和b为边的平行四边形面积,即S=|a×b|。
6、向量的运算 加法运算 向量加法的定义 已知向量a、b,在平面上任意取一点A,作AB=a,BC=b,再作向量AC,则向量AC叫做a与b的和,记做a+b,即a+b=AB+BC=AC AB+BC=AC,这种计算法则叫做向量加法的三角形法则。
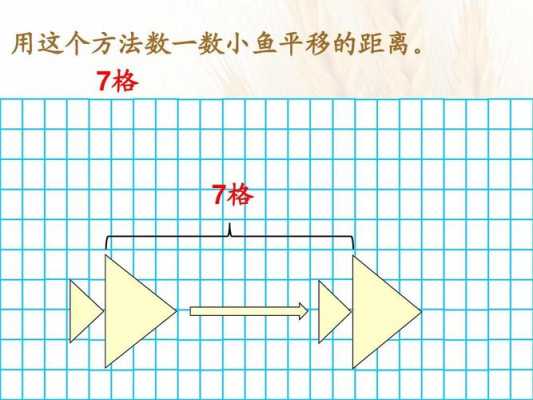
数轴向右向左平移方法
坐标平移口诀:左移,横坐标加,纵坐标不动,右移,横坐标减,纵坐标不动,上移,横坐标不动,纵坐标减,下移,横坐标不动,纵坐标加。
左右平移,x左加右减;上下平移,b上加下减。一次函数图像在x轴上的左右平移。向左平移n个单位,解析式y=kx+b变化为y=k(x+n)+b;向右平移n个单位解析式y=kx+b变化为 y=k(x-n)+b。
解:(1){1)+{2}-{3},{2}+ {1}={3}. (2)如图.最后的位置仍是点B (3){3,+{2}+{ -5, -5} ={0,0}。
解:(1){3,1}+{1,2}={4,3}, {1,2}+{3,1}={4,3};(2)①画图, 最后的位置仍是B; (3){2,3}+{3,2}+{-5,-5}={0,0}。
到此,以上就是小编对于平移法怎么用的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏