本篇目录:
二元一次方程组
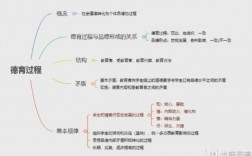
1、二元一次方程组是指含有两个未知数,并且所含未知数的项的次数都是1的方程组。知识扩展 首先,从代数的角度来看 二元一次方程具有以下形式:ax+bx+c=0,其中a、b、c为常数且a≠0。
2、二元一次方程是指含有两个未知数(例如x和y),并且所含未知数的项的次数都是1的方程。两个结合在一起的共含有两个未知数的一次方程叫二元一次方程组。每个方程可化简为ax+by=c的形式。
3、如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫做二元一次方程,有无穷个解,若加条件限定有有限个解。二元一次方程组,则一般有一个解,有时没有解,有时有无数个解。
4、二元一次方程组的解:二元一次方程组的两个公共解,叫做二元一次方程组的解。消元:将方程组中的未知数个数由多化少,逐一解决的想法,叫做消元思想。消元的方法有两种:代入消元法。加减消元法。
5、有几个方程组成的一组方程叫做方程组。如果方程组中含有两个未知数,且含未知数的项的次数都是一次,那么这样的方程组叫做二元一次方程组。
急!用更相减损术求27090、21672、8127的最大公约数
通过不断迭代这一过程,直至余数为0,即可得到最大公约数。更相减损术:更相减损术是另一种计算最大公约数的方法。它基于一个观察:两个整数a和b(其中ab),它们的最大公约数等于ab的最大公约数。

辗转相除法是求两个自然数的最大公约数的一种方法,也叫欧几里德算法。
最后所得的那个最大公约数,就是所有这些数的最大公约数。更相减损法 也叫更相减损术,是出自《九章算术》的一种求最大公约数的算法,它原本是为约分而设计的,但它适用于任何需要求最大公约数的场合。
更相减损法有点类似于求最大公约数的Stein算法。在更相减损法中,若两个是偶数则同除以2,结果乘以2。
一次函数题的解题思路、过程
在解决一次函数相关问题过程中,还会运用到许多重要的数学思想方法:数形结合思想:根据数和形之间的对应关系,将数字和图形结合起来以解决数学问题,兼备了直观性和严密性的特征。

一次函数应用题解题技巧:应用题的解法一般包括解,设,求,
解题过程如下:①首先 是奇函数 ,图像关于零点对称 ② 然后与y=x的图像关于y轴对称 ,斜率相反。
首先:弄懂X轴和Y轴的含义。其次:要弄清楚图像描述的是行程中追及问题,还是相遇问题。再次:解决问题时既可以用函数方法去解,又可以使用算数方法解决。所以在考场中,仔细审题选择比较简单的方法解决省时省力。
一次函数:形如y=kx+b(k≠0,k,b是常数)的函数叫做一次函数,是目前最简单的函数,图像为一条直线,通常具体题型有求解析式,求与坐标轴围成图形面积,两条左边轴交点坐标,实际应用问题,再难一点就是找规侓题等。
解一次函数最简单的方法是代入法,把已知的两对自变量和应变量的值代入,求得函数关系式,用代入法解一次函数的过程,实际就是解一个二元一次方程组,一次函数的要求就是一次项的系数不为0。
27×(3+100)简便运算过程?
1、简便运算如下:103×27 =(100+3)×27 =100×27+3×27 =2700+81 =2781 这道题主要运用了乘法分配律的运算方法。先找出接近100的数字103,然后进行拆分,利用分配律进行简算即可。
2、(三)运用乘法分配律进行简算,遇到除以一个数,先化为乘以一个数的倒数,再分配。如:5×(100+0.4),还应注意,有些题目是运用分配律的逆运算来简算:即提取公因数。如:0.93×67+33×0.93。
3、这道题的简便计算方法是:72*27/(8*3)=(72/8)(27/3)=9*9=81。
4、口算过程可以这样写。把122分解:100×3等于300,20×3等于60,2×3等于6 这样再加起来就是366:300+60+6。
到此,以上就是小编对于化简811881的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏