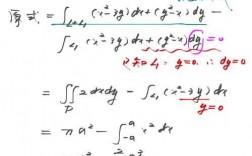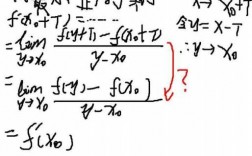本篇目录:
高数极限要详细过程?
(1)当分母的极限是“0”,而分子的极限不是“0”时,不能直接用极限的商的运算法则,而应利用无穷大与无穷小的互为倒数的关系,先求其的极限,从而得出f(x)的极限。
答案是:e^(1/6)我的过程是利用洛必达法则。

方法2,用“有界量乘无穷小量还是无穷小量”间接证明:显然,cosn是有界量,然后参照方法1用定义证明lim(n-无穷)(n+2)/(n-2)=0,即得证。用定义证明极限的关键是“适当的放缩”,放缩的方法不是唯一的。
对于如图的高等数学求极限,解答的详细过程,请看上图。此高等数学求出的极限值等于8。高等数学求极限,图中题解答的方法,是分子分母利用等价无穷小代替求极限的方法。
关于这道高等数学求极限问题,求极限的过程见上图。求这道高等数学极限时,用到泰勒公式,即我图中在求极限的前三行。对于这道高等数学求极限时,第一步,换元,即t=1/x,化为对t的极限问题,然后,通分。
高数没有八个重要极限公式,只有两个。第一个重要极限的公式:lim sinx / x = 1 (x-0)当x→0时,sin / x的极限等于1;特别注意的是x→∞时,1 / x是无穷小,无穷小的性质得到的极限是0。

高数,求极限过程
1、使用两个重要极限=1和(1+)=e求极限时,关键在于对所给的函数或数列作适当的变形,使之具有相应的形式,有时也可通过变量替换使问题简化。
2、答案是:e^(1/6)我的过程是利用洛必达法则。
3、高数求极限方法:01 定义法。此法一般用于极限的证明题,计算题很少用到,但仍应熟练掌握,不重视基础知识、基本概念的掌握对整个复习过程都是不利的。02 洛必达法则。
4、=e^{lim(x-0)[2/((1+2x)(1+x))]} (0/0型极限,应用罗比达法则)=e^2 =e。

高数求极限,数学高手帮帮忙,要详细的步骤。。谢谢
=e^{lim(x-0)[2/((1+2x)(1+x))]} (0/0型极限,应用罗比达法则)=e^2 =e。
高数求极限,数学高手帮帮忙,要详细的步骤。
/x趋于负无穷,所以e^(1/x)趋于0,此时 f(x)的极限为-1,。而当x趋于0+时,1/x趋于正无穷,所以e^(1/x)趋于正无穷,此时f(x)的极限为1。由于两个极限不相等,所以f(x)在0处的极限不存在。
高数求极限,请详细过程
使用两个重要极限=1和(1+)=e求极限时,关键在于对所给的函数或数列作适当的变形,使之具有相应的形式,有时也可通过变量替换使问题简化。
答案是:e^(1/6)我的过程是利用洛必达法则。
对于如图高等数学,这个极限求的详细过程见上图。高等数学,这个极限求的方法,主要就是用我图中注的部分公式,即第二个重要极限。如图这个极限求时,令y=1+x,然后用第二个重要极限,就可以得出此题极限。
请看上图。此高等数学求出的极限值等于8。高等数学求极限,图中题解答的方法,是分子分母利用等价无穷小代替求极限的方法。求极限时,此高等数学,解答时用的等价无穷小代替公式,见我图中的注的部分。
到此,以上就是小编对于高数极限计算的21种主要方法的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏