本篇目录:
- 1、反解方程,解出x?
- 2、求函数反函数的步骤
- 3、求反函数的时候怎么反解
- 4、用反解法写下详细过程
- 5、求反解过程
反解方程,解出x?
1、求反函数的步骤:利用反解方程,将x看成未知数,y看成已知数,解出x的值。将这个式子中的x,y兑换位置,就得到反函数的解析式。求反函数的定义域。
2、求反函数技巧:利用反解方程,将x看成未知数,y看成已知数,解出x的值。将式子中的x,y兑换位置,就得到反函数的解析式。求反函数的定义域。

3、从y=f(x)中解出 x=g(y);交换 x=g(y)中x与y的位置得到y=g(x),以B为定义域的函数y=g(x)即为所求的反函数。
求函数反函数的步骤
确定函数的定义域和值域 确定函数的定义域和值域是求反函数的第一步。定义域是函数输入的取值范围,值域是函数输出的取值范围。
求反函数的步骤:反解方程,将x看成未知数,y看成已知数,解出x的值。将这个式子中的x,y兑换位置,就得到反函数的解析式。求反函数的定义域,这个是很重要的一点,反函数的定义域是原函数的值域。
要求一个函数的反函数,通常需要遵循以下步骤:确定原函数的定义域和值域 要求反函数,首先需要明确原函数的定义域和值域。这是为了确保反函数的定义是有效的。

关于求反函数步骤如下:确定定义域和值域:首先,确定原函数的定义域和值域。定义域是指使原函数有意义的所有可能输入值的集合,而值域是指原函数的所有可能输出值的集合。
求反函数的时候怎么反解
1、求反函数的方法只有1种。那就是反解方程,对换xy位置,求定义域。求反函数的步骤:利用反解方程,将x看成未知数,y看成已知数,解出x的值。将这个式子中的x,y兑换位置,就得到反函数的解析式。
2、有的书上给出了一般步骤:确定函数y=f(x)的值域B;从y=f(x)中解出 x=g(y);交换 x=g(y)中x与y的位置得到y=g(x),以B为定义域的函数y=g(x)即为所求的反函数。
3、确定原函数的值域,也就是反函数的定义域。由y=f(x)的解析式求出x=f-1(y)。将x,y对换,得反函数的习惯表达式y=f-1(x),并注明定义域。
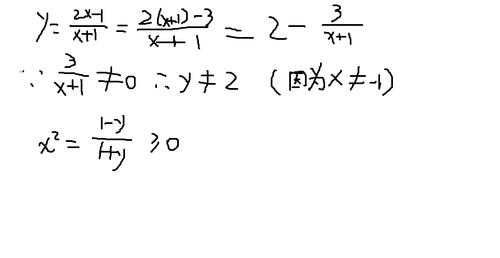
4、运用反演规则可以很方便地求出一个函数的反函数,但使用反演规则时应注意保持原函数式中运算的优先顺序不变。
用反解法写下详细过程
1、第一问,你得到R的关于k的坐标,然后可以设R坐标为(x,y),然后用x表示k,再带入y中,就可求出来轨迹啦,结果是2x^2-2x+y^2=0。这是反解法。
2、配方法反解法分离常数法判别式法换元法不等式法函数有界性法直接求函数的值域困难时,可以利用已学过函数的有界性,反客为主来确定函数的值域。
3、首先分析集合A: (x-1)*(x-4)0 解为: x1 或者 x4 接下来分析B: 根据A∩B≠空集 判定 B的方程式中x 肯定有解,并且解呢在 集合A 中。
求反解过程
求反函数的步骤:利用反解方程,将x看成未知数,y看成已知数,解出x的值。将这个式子中的x,y兑换位置,就得到反函数的解析式。求反函数的定义域。
求函数的反函数步骤如下:确定函数的定义域和值域 确定函数的定义域和值域是求反函数的第一步。定义域是函数输入的取值范围,值域是函数输出的取值范围。
反函数x=f-1(y)的定义域、值域分别是函数y=f(x)的值域、定义域。最具有代表性的反函数就是对数函数与指数函数,三角函数和反三角函数等。求反函数技巧:利用反解方程,将x看成未知数,y看成已知数,解出x的值。
/(y-1)这一步,由自变量x要有意义,故分母y-1≠0,所以才有y≠1 ,而在(y-1)x=2y-3时,根本看不出y是否可以等于1。
到此,以上就是小编对于反解法的一般步骤的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏