本篇目录：

• 1、指数分布函数怎么求?
• 2、CCD噪声分类
• 3、二项分布与泊松分布的区别
• 4、泊松分布怎么来的?推导过程?
• 5、第一题怎么做?
• 6、请问概率中的泊松分布怎么理解,公式是什么?

指数分布函数怎么求?

1、指数分布的分布函数是=1/λ，σ2=1/λ2。指数分布的分布函数公式是=1/λ，σ2=1/λ2。

2、指数分布是一种连续概率分布，它的概率密度函数为：f(x) = λe^(-λx)，其中x = 0，λ 0。指数分布的分布函数是通过对概率密度函数进行积分得到的，即：F(x) = ∫f(t)dt，从0到x。

3、指数分布公式为f(x)=λexp(-λx)。

4、是积分得到的，对密度函数从负无穷到x积分，由于函数分段，所以分段积分，若x=0，积分为零（密度函数为零），若x0，先从负无穷到零积分等于零，再从零到x积分得到分布函数的形式。

CCD噪声分类

是的，工业相机按照芯片结构分类：CCD相机 和 CMOS相机。

数码相机的相片才有“噪声”，全称是“热噪声”。是一些由红、绿、蓝三色组成的不规则且无规律的细小斑点，是一种感光元件在感光后紧接着的采集信息时因工作温度高而产生的“误码”。

视频信号连接到监视器或电视机的视频输入端便可以看到与原始图像相同的视频图像。CCD摄像机的分类 一按照成像色彩划分 CCD摄像机按成像色彩划分为彩色摄像机和黑白摄像机两种。除色度处理方面不同外，其它原理基本一致。

关于坏点：坏点是CCD在成像时产生永远发亮或发暗的死点，位置固定，根源是由于CCD当前工艺水平的局限，良品率不高造成。关于噪点：噪点是CCD在感光的时候随机产生的“噪声”，位置不固定，并且会随着环境温度升高而增多。

说到图像噪音，从数码相机的结构本身产生的噪音，到在图像处理过程中产生的噪音，实际上有各种各样的情况。这次就介绍几个主要的数码相机图像噪音问题。

进入数字时代以来，传感器技术发展了——CCD传感器和CMOS传感器两种类型。两者有什么联系和区别？首先，有一个时间差CCD出现在CMOS之前。

二项分布与泊松分布的区别

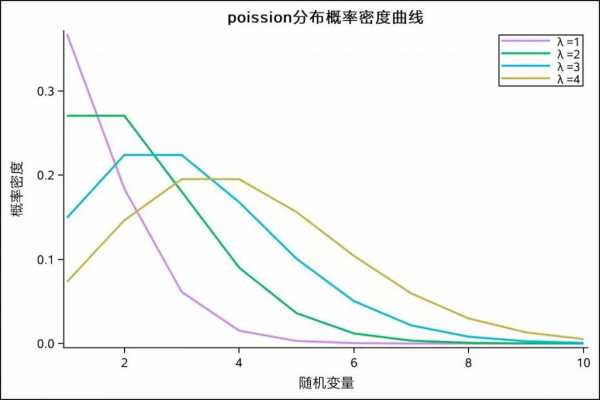
1、泊松分布的概率函数为：泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。

2、泊松分布：泊松分布适用于描述单位时间或单位面积内随机事件发生的次数。其特点是平均数等于方差，且当事件发生的概率较小、样本容量较大时，泊松分布可以近似地用于描述二项分布。

3、泊松分布和二项分布是讨论某单一变量分布的特点，泊松分布是二项分布n很大而P很小时的特殊形式。双变量分布是单变量分布向多维的推广，其讨论的是两个变量的分布情况。

4、当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np.通常当n≧10，p≦0.1时，就可以用泊松公式近似的计算。事实上，泊松分布正是由二项分布推导而来的。

5、泊松分布常用于稀有事件的发生次数的概率分析。定义 伯努利实验：只有两种可能结果的单次随机实验，其结果可能为“成功”或“失败”。

泊松分布怎么来的?推导过程?

事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。应用示例：泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。

以下是泊松分布推导过程：首先必须由二项分布引出：如果做一件事情成功的概率是 p 的话，那么独立尝试做这件事情 n 次，成功次数的分布就符合二项分布。

泊松分布的公式为：P(k)=(λ^k)*(e^(-λ))/k！。Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。

E的lamda次方泰勒展开就是N从0到无穷取和(lamda的N次方除以N的阶乘)=== 与二项分布关系 Poisson分布是二项分布n很大而P很小时的特殊形式，是两分类资料在n次实验中发生x次某种结果的概率分布。

泊松分布的推导过程 假设条件 泊松分布是基于以下假设条件的：（1）随机事件发生的概率是均匀的，即在单位时间内，随机事件发生的概率是恒定的。（2）随机事件发生是独立的，即随机事件的发生不影响其他随机事件的发生。

第一题怎么做?

1、第一题前半部分只需要合理就可以了，可以是8/7=1……1，余数可能是0，1，2，3，4，5，6。余数最大是6，因为余数不能大于除数。

2、口算这么简单，不用做。下雨了，不需要去公园玩。

3、(L/2)^2+(m-X1)^2=R^2；根据题目可以知道弦长能保持定值，为了计算上的方便可以用特殊值法。

4、神情：甜丝丝 甜津津 冷冰冰 笑嘻嘻 阴森森 苦巴巴 笑眯眯 笑哈哈 笑呵呵 笑吟吟 笑盈盈 喜洋洋 喜滋滋 喜冲冲 兴冲冲 乐悠悠 乐陶陶 乐滋滋 笑吟吟 恶狠狠 眼睁睁。

5、第一题，已经给出间断点了吧，就是x=0时，上面算式等于f(x)=-2，下面算式 f(x)=-1/2。

请问概率中的泊松分布怎么理解,公式是什么?

解析：泊松分布（Poisson distribution），台译卜瓦松分布，是一种统计与概率学里常见到的离散机率分布（discrete probability distribution），由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。

利用泊松分布公式P(x=k)=e^(-λ)*λ^k/k！P表示概率，x表示某类函数关系，k表示数量，等号的右边，λ 表示事件的频率。

泊松公式为：P(k)=(λ^k)*(e^(-λ))/k！。西莫恩·德尼·泊松（Simeon-Denis Poisson 1781～1840）法国数学家、几何学家和物理学家。1781年6月21日生于法国卢瓦雷省的皮蒂维耶，1840年4月25日卒于法国索镇。

泊松分布公式：随机变量X的概率分布为：P{X=k}=λ^k/(k！e^λ) k=0，1，..则称X服从参数为λ（λ0）的泊松分布，k代表的是变量的值，且是自然数。

泊松分布公式是Var(x)=λ。二项分布的期望E(r)=np，方差Var(r)=npq，而泊松分布的期望和方差均为λ。此时我们需要这两种分布的期望和方差相近似，即np与npq近似相等的情况。

泊松分布的公式为：P(k)=(λ^k)*(e^(-λ))/k！。Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。

到此，以上就是小编对于泊松过程的条件分布的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。