本篇目录:
- 1、关于有lnx的函数怎么求单调性,不知道做啊,大神帮帮我。。
- 2、函数y=lnx是什么意思,y=xlnx的单调减区间怎么求?
- 3、数学高手~~涵数Y=xlnx在区间(0,1)上的单调性是???
- 4、关于有lnx的函数怎么求单调性
关于有lnx的函数怎么求单调性,不知道做啊,大神帮帮我。。
在(0,1/3^(1/3))区间,函数单调减;在(1/3^(1/3),∞)区间,函数单调增。
=[xlnx -(x+1)ln(x+1)]/[x(x+1)lnx]令 g(x)=xlnx,则g(x)=lnx +1,令g(x)0,解得 x1/e,所以 g(x)在(1/e,+∞)是增函数。
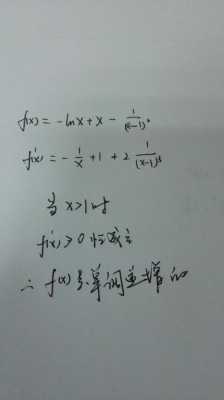
/e)时,f‘(x)=lnx+10,所以 f(x)在区间(0,1/e)递减;当x属于[1/e,+无穷)时,f‘(x)=lnx+1 0,所以f(x)在区间[1/e,+无穷)递增。所以当x=1/e时,函数f(x)有最小值 -1/e。
用你知道的说,就是 y=lnx=lgx/lge。其中e为自然对数的底,约等于.由上式,lnx与lgx单调性相同,在定义域(0,+∞)同为单调递增,而x在(0,+∞)上单调且不变号,则不影响lnx的单调性。
赞同楼上方法。其实函数向加减可以用坐标变换解释。lnx+(-x),楼主可以想象lnx上每个点都有一根线拴在x轴对应点上,然后将x轴顺时针转45度(即f(x)=-x)得到的就是所求的图形。
y=1/xlnx 对其求导,y=(1-lnx)/(xlnx)^2 当1-lnx0,即xe时,y‘0,则y在xe区域内为增函数。当1-lnx0,即xe时,y‘0,则y在xe区域内为减函数。
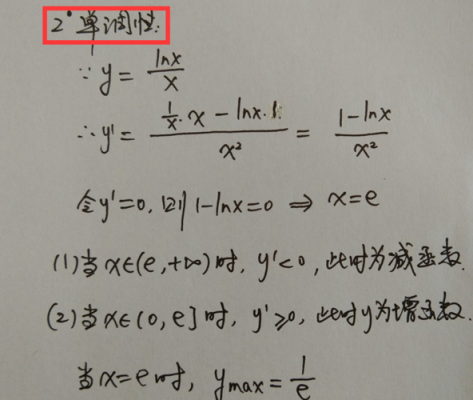
函数y=lnx是什么意思,y=xlnx的单调减区间怎么求?
函数 y = ln(x) 表示自然对数函数,其中 x 表示函数的输入值,y 表示函数的输出值。
ln为一个算符,意思是求自然对数,即以e为底的对数。e是一个常数,等于71828183…lnx可以理解为ln(x),即以e为底x的对数,也就是求e的多少次方等于x。
y=lnx是一个函数,对数函数。对数函数:对数的定义:一般地,如果ax=N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
数学高手~~涵数Y=xlnx在区间(0,1)上的单调性是???
1、解:求导:y=lnx+x/x=lnx+1。导函数在0~1上先负后正,所以原函数先减后增。并且极小值点出现在lnx+1=0,即x=e^(-1)处。

2、函数y=x+lnx,定义域为(0,正无穷大)。
3、y=lnx=lgx/lge。其中e为自然对数的底,约等于.由上式,lnx与lgx单调性相同,在定义域(0,+∞)同为单调递增,而x在(0,+∞)上单调且不变号,则不影响lnx的单调性。
关于有lnx的函数怎么求单调性
在(0,1/3^(1/3))区间,函数单调减;在(1/3^(1/3),∞)区间,函数单调增。
lnx=-1,x=1/e。当x属于(0,1/e)时,f‘(x)=lnx+10,所以 f(x)在区间(0,1/e)递减;当x属于[1/e,+无穷)时,f‘(x)=lnx+1 0,所以f(x)在区间[1/e,+无穷)递增。
y=lnx=lgx/lge。其中e为自然对数的底,约等于.由上式,lnx与lgx单调性相同,在定义域(0,+∞)同为单调递增,而x在(0,+∞)上单调且不变号,则不影响lnx的单调性。
y=lnx (x0)y=1/x0 所以 函数始终是递增的。
从导数来看单调性看起来更快y=lnx-1)/lnx,由此明显地以(e,+∞)增加,以(1,e)(0,1)减少。y0(同样靠近1的左侧的话,负数就会无限大,但是为什么小于0是指示器的法则)。
证明:首先求导Y=1+1/X,因X0,所以Y0,函数Y=X+lnX单调递增。
到此,以上就是小编对于lnx单调性的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏