本篇目录:
集合论的发展
1、年,策梅罗提出公理化集合论,后经改进形成无矛盾的集合论公理系统,简称ZF公理系统。简单来讲,就是把理发师从村子中的人中排除出去。这就是集合论发展的第二个阶段:公理化集合论。
2、集合论是康托尔于19世纪末创立的。它的发展经历两个阶段:1908年以前称为朴素集合论;1908年以后又产生了所谓公理集合论。

3、由哥德尔不完全性定理可知,如果ZF是无矛盾的,则在ZF中不能证明自身的无矛盾性,所以在公理集合论中只考虑相对无矛盾性问题。已经证明,如果ZF是无矛盾的,则NBG也是无矛盾的。
4、从19世纪60年代起,法国数学家康托尔承担了这一工作,他清楚地看到以往数学基础中的问题,都与无穷集合有关。康托尔的集合论的建立,不仅是数学发展史上一座高耸的里程碑,甚至还是人类思维发展史上的一座里程碑。
排列组合的发展历程
18世纪,古法国数学家蒲丰首次系统地将排列组合发展成独立学科,并将其定名为“组合学”。 19世纪,中法双方数学家大量发表文章,推进了排列组合的研究。
排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。 排列组合与古典概率论关系密切。发展历程:虽然数学始于结绳计数的远古时代,由于那时社会的生产水平的发展尚处于低级阶段,谈不上有什么技巧。
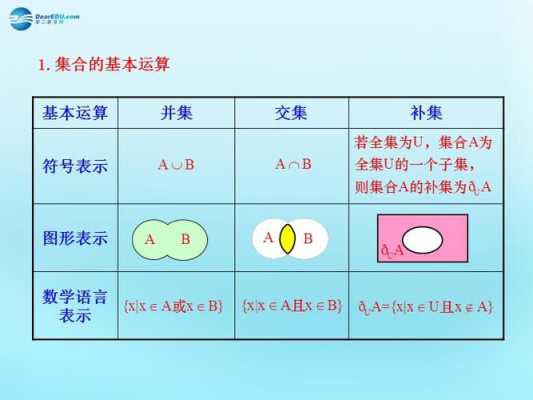
排列组合的发展历程:根据组合学研究与发展的现状,它可以分为如下五个分支:经典组合学、组合设计、组合序、图与超图和组合多面形与最优化。
取4张均为不同花色:13*13*13*13=28561种。(解析:就是同色的13张取1张,就有13种;4个种花色都要取,就是13*13*13*13)。因此概率为:28561÷270725×100%≈55%。
排列组合发展历程 虽然数学始于结绳计数的远古时代,由于那时社会的生产水平的发展尚处于低级阶段,谈不上有什么技巧。
数学发展史时间轴
1、一般分为:数学的萌芽时期;常量数学时期;变量数学时期;现代数学时期。数学起源于人类早期的生产活动,为古中国六艺之一,亦被古希腊学者视为哲学之起点。数学最早用于人们计数、天文、度量甚至是贸易的需要。

2、算法的发展史(时间轴)公元前 4000 年 - 在这儿,我们必须提到远古的苏美尔人。
3、一般长为13--14cm,径粗0.2~0.3cm,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带。
集合论的起源
集合论的基本理论创立于19世纪,关于集合的最简单的说法则是在朴素集合论(最原始的集合论)中的定义,即集合是“确定的一堆东西”,集合里的“东西”则称为元素。
3年11月29日康托尔在给戴德金(1831-1916)的一封信中,终于把导致集合论产生的问题明确地提了出来:正整数的集合(n)与实数的集合(x)之间能否把它们一一对应起来。
集合论的基础是由德国数学家康托尔在19世纪70年代奠定的,经过一大批科学家半个世纪的努力,到20世纪20年代已确立了其在现代数学理论体系中的基础地位,可以说,现代数学各个分支的几乎所有成果都构筑在严格的集合理论上。
HITS 算法使用一个基于文本的搜索引擎,得到许多被返回的页面,构成根集合(root set)R。
具体地,有用来探索由数学核心至其他领域上之间的连结的子领域:由逻辑、集合论(数学基础)、至不同科学的经验上的数学(应用数学)、以较近代的对于不确定性的研究(混沌、模糊数学)。
到此,以上就是小编对于集合的发展过程是什么的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏