本篇目录:
- 1、做数学证明题的思路是什么,过程怎么写
- 2、SSAT数学题,求助,好的加分。要步骤讲解
- 3、数学归纳法的证明过程是怎样的?
- 4、数学,求证明过程
- 5、数学中的证明题、证明(的过程)、公式的推导用英语分别怎么说?_百度...
- 6、已知A是一个n阶对称矩阵,B是一个n阶反对称矩阵,证明AB-BA是一个对称...
做数学证明题的思路是什么,过程怎么写
1、一个证明题目中,可以分成两部分,已知条件(这点就要自己细心分析了,包括基础知识的变形啊、基本功啊、数学模型建模啊等)和求证结论。
2、几何证明题入门难,证明题难做,是许多学生在学习中的共识,这里面有很多因素,有主观的、也有客观的,学习不得法,没有适当的解题思路则是其中的一个重要原因。

3、),推导型证明。几何证明很多看起来那简直非人所想,所以很难说有基本的思路和步骤,尤其那神奇的辅助线!这也是几何原本的魅力。但要做到基本,还是回归到基础概念,什么中位线,平行线,三角形四心等。
4、最后,建议你平时多做相关题目,积累经验,培养数感,大胆地和老师交流 首先你要把老师讲的定理啊什么的记牢一点,做到了这一点你就要多做课外题了。
SSAT数学题,求助,好的加分。要步骤讲解
那个数可以写成4*N+1的形式,N是整数。当然只有93=23*4+f是任意不为0的数,下面那个为真?如果考虑到无穷数,II,III不对吧。选A。
首先必须求得入射点的坐标,然后根据两点确定一条直线则可以将入射光线和反射光线分别求得。
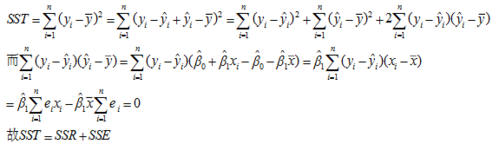
数学归纳法的证明过程是怎样的?
一般地,证明一个与自然数n有关的命题P(n),有如下步骤:(1)证明当n取第一个值n0时命题成立。
(归纳奠基)证明当n取第一个值n0(n0∈N*)时命题成立;(归纳递推)假设n=k(k≥n0,k∈N*)时命题成立,证明当n=k+1时命题也成立。
数学归纳法一般步骤1 先证明n=1时的情况,很简单 2 设n=m时成立,将m代入原式得一个等式 3 将n=m+1代入原式左边,展开,化简,想办法往n=m的右边的形式靠,然后将n=m代入进去,再化简,最后得出n=m+1。
从严格的数学角度来说,数学归纳法是一个严格的数学定理,注意不是公理。它是可以在集合论的一系列公理下被证明的。证明如下:数学归纳法对解题的形式要求严格,数学归纳法解题过程中:第一步:验证n取第一个自然数时成立。

数学,求证明过程
角CAF=BAF,在三角形CAF中,角CFA=180-ACF-CAF=90-CAF 在三角形AED中,角AED=90-EAD。因为AF是角平分线,所以角AED=CFA,因为对顶角,所以CEF=CFE。
再如2005年数学一第18题(1)是关于零点存在定理的证明题,只要在直角坐标系中结合所给条件作出函数y=f(x)及y=1-x在[0,1]上的图形就立刻能看到两个函数图形有交点,这就是所证结论,重要的是写出推理过程。
(1)证明:所以∠EAB=∠DAC,又EA=DA,BA=CA,故ΔAEB≌ΔADC。于是∠EBC=∠EBA+∠ABC=∠DCA+∠ABC=120°。那么∠EBC+∠BCG=120°+60°=180°,于是EB//GC,又EG//BC,故BCGE为一平行四边形。
数学中的证明题、证明(的过程)、公式的推导用英语分别怎么说?_百度...
proof:证明 since...,...hence,因此。。(我们可得知)。。
请各举一个例子说明英语中的主动语态和被动语态,急啊! 英语动词有两种语态:主动语态和被动语态。主动语态表示主语是动作的执行者,被动语态表示主语是动作的承受者。
数学证明题模板怎么写如下:命题表述:明确要证明的命题是什么。假设或前提条件:在证明过程中需要依赖某些假设或前提条件,需要明确列出。证明过程:通过逻辑推理和演绎,一步步证明命题的正确性。
下面给大家分享一些关于做题技巧数学初中几何证明题,希望对大家有所帮助。证明两线段相等 两全等三角形中对应边相等。同一三角形中等角对等边。等腰三角形顶角的平分线或底边的高平分底边。
理解定理和公式:在数学证明题中,我们需要应用各种定理和公式。因此,我们需要充分理解定理和公式,及其推导过程。这样才能在证明的过程中正确灵活地应用各种定理和公式。
平面几何中讲的面积公式以及由面积公式推出的与面积计算有关的性质定理,不仅可用于计算面积,而且用它来证明平面几何题有时会收到事半功倍的效果。
已知A是一个n阶对称矩阵,B是一个n阶反对称矩阵,证明AB-BA是一个对称...
1、因为A=-AT,B=BT,所以:(AB-BA)T=(AB)T-(BA)T=BTAT-ATBT=B*(-A)+A*B=AB-BA,即(AB-BA)T=AB-BA 所以AB-BA是n阶对称矩阵。
2、不是反对称矩阵。因为A^T=A,B^T=-B,所以(BAB)^T=(B^T)(A^T)(B^T)=(-B)A(-B)=BAB,即BAB是对称矩阵。
3、正定矩阵定义:对于任意非零向量x=(x1,x2,...,xn)^t,都满足x^tax0,则a为正定矩阵。设x为任意n维列向量,x^t(a-b^2)x=x^tax-x^tb^2x,b^2=b*b,由于b为反对称矩阵,b=-b^t。
4、已知A、B是n阶对称矩阵时,A=A^T B=B^T,若AB=BA,两边转置有:(AB)^T=(BA)^T 即:(AB)^T=A^TB^T,故AB=BA,原命题成立。对称矩阵是元素以对角线为对称轴对应相等的矩阵。
5、yajun宝贝 ,你好:由反对称矩阵定义知有B=-B^T,于是A-B^TB=A+B^2,由正负矩阵的定义有X^TAX0,于是X^T(A-B^TB)X=X^TAX-X^TB^TBX=X^TAX+(B^TX)20,故是正定矩阵。
6、任意一个n阶方阵A都可以表示为一个n阶对称矩阵与一个n阶反对称矩阵之和是正确的。
到此,以上就是小编对于如何证明sst=ssa+sse的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏