本篇目录:
- 1、函数极限,过程谢谢
- 2、求极限的方法归纳,具体点
- 3、求函数极限的几种方法
- 4、函数如何求极限?
函数极限,过程谢谢
1、则极限值不存在,因为无穷就是不存在,-无穷,就是表示极限值不存在。就像y=x,y属于(-无穷,+无穷)再R商的至于,向上-+无穷,即不存在最大值,向下--无穷,即不存在最小值,上阶和下嫁诶都不存在,即无界函数。
2、这个是不定积分,不是极限。很明显令x = a * sinθ是最快捷的方法。

3、原式=1 重要极限:第一个:x趋近于0时,sinx/x的极限为1第二个:n趋近于无穷大时,(1+1/n)的n次方的极限为e。
4、对数法。此法适用于指数函数的极限形式,指数越是复杂的函数,越能体现对数法在求极限中的简便性,计算到最后要注意代回以e为底,不能功亏一篑。定积分法。
求极限的方法归纳,具体点
1、求极限的方法有以下几种:代入法:将变量代入函数中,得到一个数值,即为该点的函数值。夹逼定理:通过夹逼定理找到一个上下界,并让上下界无限逼近目标点,从而得到极限值。
2、未定式求极限(1)分子、分母都趋向无穷大,即型,处理方法是分子、分母同除无穷大因子的最高次幂。(2)分子,分母都趋向无穷小,即型,常见的处理方法是:消零因子,有理化,利用重要极限公式或等价无穷小替换。
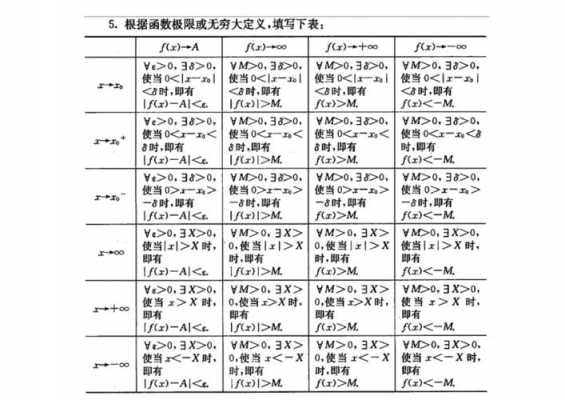
3、夹挤法。这不是普遍方法,因为不可能放大、缩小后的结果都一样。特殊情况下,化为积分计算。其他极为特殊而不能普遍使用的方法。
4、用洛必达法则,针对0/0型或无穷/无穷型,对分子分母同时求导后求极限的方法。利用泰勒公式求极限的方法。还有把极限化为导数或积分求极限的方法等。
5、求极限的方法有:通过等价无穷小替换来求极限、通过第一个重要极限来求极限、通过第二个重要极限来求极限、通过洛必达法则来求极限、通过夹逼定理来求极限等。本文详细的介绍上述求极限的方法。
6、求极限基本方法有:分式中,分子分母同除以最高次,化无穷大为无穷小计算,无穷小直接以0代入。无穷大根式减去无穷大根式时,分子有理化。

求函数极限的几种方法
**代入法(直接代入):** 对于绝大多数简单的函数,可以直接将该点的值代入函数中,得到极限值。这对于多项式函数、指数函数和三角函数等基本函数非常有效。 **因子分解法:** 通过因式分解函数,可以简化计算。
求极限的方法有以下几种:代入法:将变量代入函数中,得到一个数值,即为该点的函数值。夹逼定理:通过夹逼定理找到一个上下界,并让上下界无限逼近目标点,从而得到极限值。
求极限的常用方法如下:利用函数的连续性求函数的极限(直接带入即可)如果是初等函数,且点在的定义区间内,那么,因此计算当时的极限,只要计算对应的函数值就可以了。
其中,最常用的方法是洛必达法则,等价无穷小代换,两个重要极限公式。在做题时,如果是分子或分母的一个因子部分,如果在某一过程中,可以得出一个不为0的常数值时,我们常用数值直接代替,进行化简。
求极限基本方法有:分式中,分子分母同除以最高次,化无穷大为无穷小计算,无穷小直接以0代入。无穷大根式减去无穷大根式时,分子有理化。
函数如何求极限?
要求函数的极限,可以按照以下步骤进行: 确定自变量趋近的极限点。找到自变量趋近的点,通常是无穷大或某个特定值。这个极限点通常用符号表示,如 x → a 或 x → ±∞。 使用极限运算法则。
求函数的极限可以按照以下步骤进行:确定函数的形式和变量。根据函数的类型,选择适当的求极限的方法。利用求极限的方法计算函数的极限值。
求函数极限,有以下一些常见的方法: 替换法:将x逐渐逼近极限值进行代入计算,看随着x越来越逼近极限值函数值趋于什么,从而求出极限值。
到此,以上就是小编对于6个函数极限的定义的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏