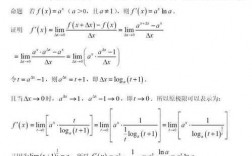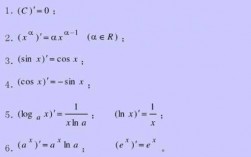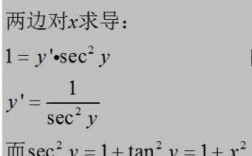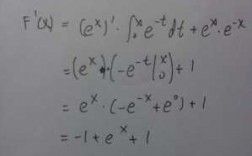本篇目录:
- 1、如何求导数
- 2、求导的三个基本步骤
- 3、函数求导数的方法
- 4、如何求一个函数的导数?
如何求导数
1、求导数方法如下:第一步:确定函数的定义域.如本题函数的定义域为R。第二步:求f(x)的导数f′(x)。第三步:求方程f′(x)=0的根。
2、常函数即常数y=c(c为常数),y=0 。 幂函数y=x^n,y=n*x^(n-1)(n∈R) 。 基本导数公式3指数函数y=a^x,y=a^x * lna。 对数函数y=logaX,y=1/(xlna) (a0且a≠1,x0)。

3、求导的线性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合(即①式)。两个函数的乘积的导函数:一导乘二+一乘二导(即②式)。
4、一般说来,求导可以分为三种方法:极值法、微分法以及导数法。极值法是最简单的求导方法,它可以告诉我们函数输入新值后,输出值如何变化,借此我们可以求得函数的极值。
5、要求一个函数的导数,可以按照以下步骤进行:确定函数的表达式。假设函数为 f(x)。使用导数的定义式计算导数。
求导的三个基本步骤
使用导数定义求解导数的步骤主要分为三个步骤。这里以幂函数y=x^n为例说明。02 第一步,求出因变量的增量Δy=f(x+Δ)-f(x)。03 第二步,计算Δy与Δx的比值。

- 常数函数的导数:(c) = 0,其中c是常数。- 幂函数的导数:(x^n) = n * x^(n-1),其中n是常数。- 一次函数的导数:(ax + b) = a,其中a和b是常数。
例题:如图片所示。方程的左右两边同时求出关于x的偏导数。求出u关于x的导数,期中u为符合函数,u=f(x,y,z),x=x,y=0*x,z=(x,y)。将z关于x的导数带入u关于x的导数中。
根据导数定义,用三步法求出一些简单函数的导数。(1)求△y。(2)求:△y/△x 。
Δy = (x + h)^2 - x^2 步骤二:算比值 接下来,我们将增量Δy除以对应的x的增量,得到一个比值。比值 = Δy / h 步骤三:取极限 最后一步是求极限,即让微小的x增量 h 趋向于零。这将给我们导数的定义。

函数求导数的方法
1、(1)求函数y=f(x)在x0处导数的步骤:① 求函数的增量Δy=f(x0+Δx)-f(x0)② 求平均变化率 ③ 取极限,得导数。
2、公式法这个方法需要熟练掌握导数的基本公式。导数四则运算公式导数的乘法和除法公式要能熟练运用。
3、公式法:这个方法需要熟练掌握导数的基本公式。导数四则运算公式:导数的乘法和除法公式要能熟练运用。复合函数的链式法则--非常重要的求导方法。链式法则在应用时一般分成4步:分解-各自求导-相乘-回代。
如何求一个函数的导数?
证明函数在整个区间内连续。(初等函数在定义域内是连续的)先用求导法则求导,确保导函数在整个区间内有意义。端点和分段点用定义求导。分段点要证明左右导数均存在且相等。
求导是数学计算中的一个计算方法,它的定义就是,当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。
例题:如图片所示。方程的左右两边同时求出关于x的偏导数。求出u关于x的导数,期中u为符合函数,u=f(x,y,z),x=x,y=0*x,z=(x,y)。将z关于x的导数带入u关于x的导数中。
求函数的导数可以使用多种方法,其中的两种常用方法:求导法和定义法。求导法:求导法是一种通过利用函数的基本求导规则,将函数表示成基本函数的运算组合的方法来求导的方法。根据基本求导法则,对基本函数进行求导。
要求一个函数的导数,可以使用以下方法: 使用导数定义计算导数:根据导数的定义,函数 f(x) 在某一点 x 处的导数可以通过计算极限来求得。
导数的除法公式:(u/v)=(uv-uv)/v。求导是数学计算中的一个计算方法,导数定义为:当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。
到此,以上就是小编对于求导的几种方法的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏