本篇目录:
直角三角形斜边中线定理证明过程
设直角三角形三边长分别为AB=3,BC=4,AC=5。斜边的一半长为5,斜边上的高BE=(3*4)/5=4,在线段AE上上必能找到一点D,使BD=5,但BD并不是AC边的中线,因为AC边的中点在线段EC上。
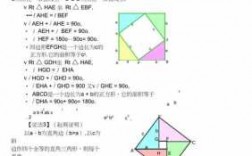
直角三角形斜边中线等于斜边的一半。设在直角三角形ABC中,∠BAC=90°,AD是斜边BC的中线,求证:AD=1/2BC。【证法1】延长AD到E,使DE=AD,连接CE。

首先,我们可以使用勾股定理来表示直角三角形的边长关系:AB+BC=AC因为BC是斜边,它对应的边长即为直角三角形的斜边长度。根据中点定理,我们知道中线将边分成两段,且两段相等。
逆定理1 如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形,且该边是斜边。几何语言:在△ABC中,AD是中线,且BC=2AD,则∠BAC=90°。
定理证明 设在直角三角形ABC中,∠BAC=90°,AD是斜边BC的中线,求证:AD=1/2BC。延长AD到E,使DE=AD,连接CE。
三角形中线定理公式
三角形中线定理公式是:三角形中线的长度等于边长一半。什么是三角形中线:在一个三角形中,连接每条边的中点所形成的线段被称为中线。一个三角形有三条中线,分别连接三个顶点的中点。

AB2+AC2=2BI2+2AI2 或作AB2+AC2=(1/2)BC+2AI。定理证明 如图,AD是△ABC的中线,AH是高线。
这个公式是AB2+AC2=2(BI2+AI2)。
中线长公式是2(m_+n_)=a_+b_。中线定理是一种数学原理,指的是三角形一条中线两侧所对的边平方和等于底边平方的一半与该边中线平方的两倍的和。
三角形中线长定理公式是2(m^2+n^2)=a^2+b^2。中线长定理,是表述三角形三边和中线长度关系的定理,具体是指三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。

中线定理即重心定理:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,中线定理为三角形ABC内BM=MC,则AB^2+AC^2=2*(AM^2+BM^2)。
直角三角形斜边中线定理推导过程
首先,我们可以使用勾股定理来表示直角三角形的边长关系:AB+BC=AC因为BC是斜边,它对应的边长即为直角三角形的斜边长度。根据中点定理,我们知道中线将边分成两段,且两段相等。
∵AD是斜边BC的中线∴BD=CD=1/2BC∵E是AC的中点∴DE是△ABC的中位线∴DE//AB(三角形的中位线平行于底边)∴∠DEC=∠BAC=90°(两直线平行,同位角相等)∴DE垂直平分AC∴AD=CD=1/2BC。
定理证明 设在直角三角形ABC中,∠BAC=90°,AD是斜边BC的中线,求证:AD=1/2BC。延长AD到E,使DE=AD,连接CE。
解:设已知直角三角形一条直角边AC边长为b,这条边所对的角度为t,利用三角函数即可求得其他两边的长度:(1)另一条直角边AB的长度c=b/tant (2)斜边CB的长度a=b/sint。
三角形中线定理怎么证明?
1、欲证DE=BC/2这种线段的倍半问题,往往可以将短的线段放大,转化为证明两线段相等,此题可将线段DE延长一倍至F,再连FC,把问题转化为证明四边形DFCB为平行四边形。
2、三角形ABC 中线为DEF,交点为O,则六块面等。
3、线段EF平行于边AB,并且长度等于边AB长度的一半。 线段FD平行于边BC,并且长度等于边BC长度的一半。
4、中位线的三种证明方法:第一种:取底边的中点,就是把底边分成两份,证明其中的一份与中位线相等。第二种:补,把中位线延长加倍,证明与底边相等。第三种:过其中一个中点作底边的平行线,证明与已知中位线重合。
到此,以上就是小编对于中线定理公式证明的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏