本篇目录:
- 1、急!!!“倍角公式”中“cos2A=cosA-sinA”证明,要详细过程
- 2、cos2x和cosx2的区别是什么?
- 3、cos2a=2cosa^2-1如何证明呢?
- 4、二倍角公式的推导过程怎么写?
急!!!“倍角公式”中“cos2A=cosA-sinA”证明,要详细过程
倍角公式:(1) sin2A=2sinAcosA 。(2) cos2A=2(cosA)^2-1=1-2(sinA)^2 。(3) tan2A=2tanA/[1-(tanA)^2]。推导过程:(1) sin2A=sin(A+A)=sinAcosA+cosAsinA=2sinAcosA。
tan2A=Sin2A/Cos2A,代入tan2A=2SinACosA/CosA^2-SinA^2。分子分母同时除以CosA^2,即可得tan2A=2tanA/(1-tanA^2)。
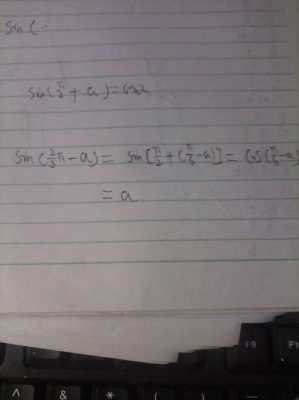
高中数学合集百度网盘下载 链接:https://pan.baidu.com/s/1znmI8mJTas01m1m03zCRfQ?pwd=1234 提取码:1234 简介:高中数学优质资料下载,包括:试题试卷、课件、教材、视频、各大名师网校合集。
cos2a=cos^2a-sin^2a=1-2sin^2a=2cos^2a-1 余弦定理亦称第二余弦定理。关于三角形边角关系的重要定理之一。该定理断言:三角形任一边的平方等于其他两边平方和减去这两边与它们夹角的余弦的积的两倍。
cos2x和cosx2的区别是什么?
相同的,只是写法不一样。具体回答如图:反余弦函数是非奇非偶函数。因为反余弦函数图像不关于y轴对称,故不是偶函数;又因为反余弦函数图像不关于原点对称,故不是奇函数。
cos(x^2)和cos^2x不一样。分析:cos(x^2)是对x的平方。cos^2x是对cosx的平方。同角三角函数的基本关系式 倒数关系:tanα ·cotα=sinα ·cscα=cosα ·secα=1。
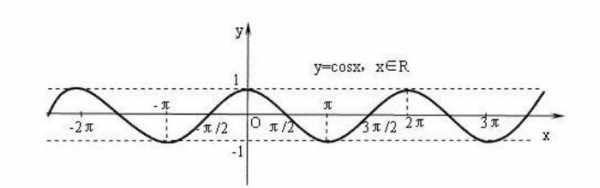
图像上,2cosx和cosx唯一的差别就是振幅是cosx的两倍,其他毫无差别。图像上,cos2x和cosx唯一的差别就是把cosx以y轴为不动轴,左右两侧图像全部向y轴压缩一半。这样也就是把周期变成了π。
cos2x=cosx-sinx=2cosx-1=1-2sinx=(1-tanx)/(1+tanx),即:cos2x=2cosx的平方-1=cosx的平方-sinx平方=1-2sinx的平方。
关系:cos2x等于2cosx的平方减去1。二倍角公式。cos x与cos2x图像关系?cosx的周期是2π,cos2x的周期是π,cosx图像上所有点的横坐标缩小为原来一半,就得到cos2x图像。
题目分析:这个式子是一种连乘的三角函数,且函数角出现倍增现象。于是我们联想 到我们学过的一个公式sin2x=2sinxcosx,应用这个公式即可求解。

cos2a=2cosa^2-1如何证明呢?
1、所用公式 cos(α+β)=cosαcosβ-sinαsinβ 当β = α 时,原式 = cos(2α)=cosαcosα-sinαsinα =cos^2(α)-sin^2(α)=2cos^2(α)-1 你题目不正确。
2、Cos2a=2Cosa^2-1 推导:cos2a=cos(a+a)=cosacosa-sinasina=(cosa)人2(sina)^2=2(cosa)^2-1=1-2(sina)^2。
3、cos2a=cos^2a-sin^2a=1-2sin^2a=2cos^2a-1 余弦定理亦称第二余弦定理。关于三角形边角关系的重要定理之一。该定理断言:三角形任一边的平方等于其他两边平方和减去这两边与它们夹角的余弦的积的两倍。
4、二倍角公式记忆法 sin2a=2sinacosa。记:二正弦二提前续余弦。cos2a=cosa2-sina2=1-2sina2=2cosa2-1。记:二余弦二提前方余弦把一减。tg2a=2tga/(1-tana平方)。
二倍角公式的推导过程怎么写?
二倍角公式:Sin2a=2Sina*Cosa Cos2a=Cosa^2-Sina^2=1-2Sina^2=2Cosa^2-1 tan2a=(2tana)/(1-tana^2)。
利用两角和公式,推导二倍角公式。详情如图所示:供参考,请笑纳。
倍角公式:(1) sin2A=2sinAcosA 。(2) cos2A=2(cosA)^2-1=1-2(sinA)^2 。(3) tan2A=2tanA/[1-(tanA)^2]。推导过程:(1) sin2A=sin(A+A)=sinAcosA+cosAsinA=2sinAcosA。
同理可以写出其他形式的三角函数的二倍角公式,大家不妨自己写一下看看。这里要提示下的是余弦的二倍角公式在写出后,然后利用sinα+cosα=1这个关系式,又可以推导出两个公式。
到此,以上就是小编对于证明cosπ2a=sina的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏