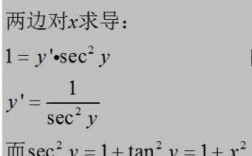本篇目录：

• 1、不定积分的过程是怎样的?
• 2、不定积分的计算过程是怎样的?
• 3、不定积分的计算?
• 4、不定积分的计算过程具体是怎样的?
• 5、不定积分怎么计算?
• 6、不定积分计算过程

不定积分的过程是怎样的?

x)在[a，b]上可积。定积分与不定积分看起来风马牛不相及，但是由于一个数学上重要的理论的支撑，使得它们有了本质的密切关系。把一个图形无限细分再累加，这似乎是不可能的事情，但是由于这个理论，可以转化为计算积分。

不定积分求解的一般方法：积分公式法：直接利用积分公式求出不定积分。换元积分法：不定积分换元积分法可分为第一类换元法与第二类换元法。第一类换元法（即凑微分法）通过凑微分，最后依托于某个积分公式。

这道高等数学不定积分求的过程见上图。求此高等数学问题，属于一阶线性微分方程问题，其中的不定积分见我图中的注的部分，用凑微分即换元法可以积分出来。然后，利用e的对数性质，就可以得出图中不定积分的结果。

不定积分怎么求 一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。

解：这个得具体情况具体分析，请把具体的不定积分公式题目发过来，我看看。最好是图片，这样比较直观方便计算。

不定积分的计算过程是怎样的?

1、x)在[a，b]上可积。定积分与不定积分看起来风马牛不相及，但是由于一个数学上重要的理论的支撑，使得它们有了本质的密切关系。把一个图形无限细分再累加，这似乎是不可能的事情，但是由于这个理论，可以转化为计算积分。

2、解：这个得具体情况具体分析，请把具体的不定积分公式题目发过来，我看看。最好是图片，这样比较直观方便计算。

3、例如本题不定积分计算过程如下：∫（1-3x）^6dx =(-1/3)∫(1-3x)^6d(1-3x)=-1/3*(1-3x)^7*(1/7)+C =-1/21*（1-3x）^7+C。

4、其中∫叫做积分号，f(x)叫做被积函数，x叫做积分变量，f(x)dx叫做被积式，C叫做积分常数，求已知函数的不定积分的过程叫做对这个函数进行积分。

不定积分的计算?

这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式）。

不定积分(indefinite integral)也称为原函数，是对于定积分( definite integral)求解的逆运算。

不定积分的计算方法：积分公式法：直接利用积分公式求出不定积分。换元积分法：换元积分法可分为第一类换元法与第二类换元法，第一类换元法通过凑微分，最后依托于某个积分公式。进而求得原不定积分。

x）+C.其中∫叫做积分号，f（x）叫做被积函数，x叫做积分变量，f（x）dx叫做被积式，C叫做积分常数，求已知函数不定积分的过程叫做对这个函数进行积分。

不定积分的计算过程具体是怎样的?

1、ln(1+x)的定积分当i=1时，i/n→0当i=n时，i/n=1所以积分区间是[0，1]。原式=lim(n-∞) n*∑(k=1-n) 1/(k^2+n^2)。=lim(n-∞) (1/n)*∑(k=1-n) 1/[(k/n)^2+1]。

2、∫(secx)^3=secx*tanx+∫secxdx ∫(secx)^3=(1/2)secx*tanx+(1/2)ln|secx+tanx|+C 不定积分的性质：一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。

3、解：这个得具体情况具体分析，请把具体的不定积分公式题目发过来，我看看。最好是图片，这样比较直观方便计算。

不定积分怎么计算?

1、积分公式法 直接利用积分公式求出不定积分。换元积分法 换元积分法可分为第一类换元法与第二类换元法。第一类换元法（即凑微分法）通过凑微分，最后依托于某个积分公式。进而求得原不定积分。

2、常用不定积分公式如下：∫0dx=c。∫x^udx=(x^(u+1))/(u+1)+c。∫1/xdx=ln|x|+c。∫a^xdx=(a^x)/lna+c。∫e^xdx=e^x+c。∫sinxdx=-cosx+c。不定积分其他情况简介。

3、计算方法如下：这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式）。

不定积分计算过程

x）+C.其中∫叫做积分号，f（x）叫做被积函数，x叫做积分变量，f（x）dx叫做被积式，C叫做积分常数，求已知函数不定积分的过程叫做对这个函数进行积分。

例如本题不定积分计算过程如下：∫（1-3x）^6dx =(-1/3)∫(1-3x)^6d(1-3x)=-1/3*(1-3x)^7*(1/7)+C =-1/21*（1-3x）^7+C。

其中F是f的不定积分。这样，许多函数的定积分的计算就可以简便地通过求不定积分来进行。不定积分只是导数的逆运算，所以也叫做反导数。而定积分是求一个函数的图形在一个闭区间上和 x 坐标轴围成的面积。

不定积分的计算方法如下：凑微分法：把被积分式凑成某个函数的微分的积分方法。换元法：包括整体换元，部分换元等等。分部积分法：利用两个相乘函数的微分公式，将所要求的积分转化为另外较为简单的函数的积分。

到此，以上就是小编对于不定积分步骤的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。