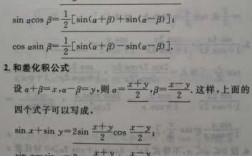本篇目录:
快求“两角和与差的正弦,余弦和正切公式”的推导步骤
两角差的余弦公式推导是:cos(α-β)=cosαcosβ+sinαsinβ。
sin(a+b)=sinacosb+cosasinb令a=b即:sin2a=2sinacosa cos(a+b)=cosacosb-sinasinb令a=b即:cos2a=cosa的平方-sina的平方关键在于角的变换,平时需要自己多揣摩。平时要多做点数学题目。

诱导公式:(kπ)/2±α,其中k为奇数时,正弦变余弦,余弦变正弦,正切变余切,余切变正切;符号看象限。k为偶数时,函数名称不变。简记为:奇变偶不变,符号看象限。
先利用单位圆(向量)推到两角和与差的余弦公式,再利用诱导公式推导正弦公式,最后利用同角三角函数的基本关系推到正切公式。
两角和与差的余弦正弦正切公式如下:sin(α±β)=sinα·cosβ±cosα·sinβ,cos(α+β)=cosα·cosβ-sinα·sinβ,tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)。
正弦,余弦和差公式是怎样推倒出来的
1、可以用向量的方法推出来,在单位圆上任意取两点A(cosa,sina),B(cosb,sinb),则向量OA=(cosa,sina),向量OB=(cosb,sinb),OA和OB的夹角的余弦值cos(a-b)=OA*OB/(|OA|*|OB|)=cosa*cosb+sina*sinb。

2、先利用单位圆(向量)推到两角和与差的余弦公式,再利用诱导公式推导正弦公式,最后利用同角三角函数的基本关系推到正切公式。
3、两角差的余弦公式推导是:cos(α-β)=cosαcosβ+sinαsinβ。
4、令 a=b,由(3)式,得到 tan(2a)=(2*tan a)/[1-(tan a)^2].这就是正切弦函数的二倍角公式。切割化弦公式 也就是普通的正割余割或者正切余切转化成正弦余弦的公式。
5、诱导公式:(kπ)/2±α,其中k为奇数时,正弦变余弦,余弦变正弦,正切变余切,余切变正切;符号看象限。k为偶数时,函数名称不变。简记为:奇变偶不变,符号看象限。

6、(以下是推论的证明,托勒密定理可视作特殊情况。
余弦公式怎么推导?
cosB=(c2+a2-b2)/2ac。余弦定理的定义和常见变形:余弦定理 三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
b = a + c - 2ac*cos(B)其中,c = a + b - 2ab*cos(C) 表示c边两边的平方等于另外两条边平方的和减去这两边的乘积与夹角C的余弦的乘积。
两角差的余弦公式推导是:cos(α-β)=cosαcosβ+sinαsinβ。
余弦公式:cosA=(b+c-a)/2bc。
由余弦定理公式推导出:cos A=(b+c-a)/2bc。
怎样用平面向量推正余弦和差角公式?
1、先利用单位圆(向量)推到两角和与差的余弦公式,再利用诱导公式推导正弦公式,最后利用同角三角函数的基本关系推到正切公式。
2、正余弦定理在定理的发现、应用中没有涉及平面向量的影子。
3、线线角可以直接采用如下公式求取,因为线线角范围是(0,π/2],因此其夹角的正弦值和余弦值均恒大于等于零,所以直接求绝对值即可。
4、设三角形ABC的三边长分别是a,b,c。以A为原点,AB方向为x轴正向。
5、差角的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ。余弦定理是欧氏平面几何学基本定理。
6、用两角差的余弦公式推导两角和的余弦公式。两角差的余弦公式推导过程。两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ。可以用:向量法,两点间距离法,复数法,高斯公式法,几何法推导。
到此,以上就是小编对于余弦求和公式推导过程的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏