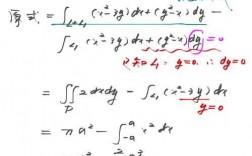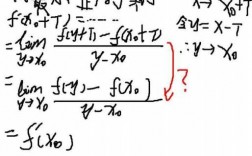本篇目录：

• 1、高数题,请教一下详细的解答过程
• 2、解释高数题解题步骤?
• 3、高数解题,要解题步骤
• 4、高数求详细解题步骤
• 5、高数。求解答过程,谢谢。

高数题,请教一下详细的解答过程

。证明方程x+x-1=0在[0，1]内只有一个实根。

先上第一小题 未完待续 第二小题如下：供参考，请笑纳。

第一题首先要知道对变上限积分求导的公式，然后对极限运用洛必达法则求解即可。第二题不要直接去积分，首先判断被积函数是奇函数，还是偶函数，若为奇函数，并且上下限互为相反数，则该积分结果就是0。

因为f(x)在[a，b]连续，在(a，b)可导，且f(a)=f(c)=0，由罗尔中值定理可知存在d∈(a，c)使得f(d)=0。而(a，c)包含于(a，b)，即f(x)在(a，b)内至少有一个根。

解释高数题解题步骤?

1、首先，计算待证明极限的表达式与极限值之差的绝对值，即xn-2/3的绝对值表达式；如果假设有一个足够小的E，总能找到一个N，使计算式在n比这个N大后，前述绝对值的表达式一定小于E。得到极限值的证明。

2、高数问题解答过程，见上图。这道高数问题的第一题，第一步用等价，等价后代入，即得。高数问题的第二题，第一步用有理化，然后化简，再代入即得。具体的求高数问题解答过程见上。

3、掌握解题步骤是解答应用题的第一步，要想掌握解答应用题的技能技巧，还需要掌握解答应用题的基本方法。一般可以分为综合法、分析法、图解法、演示法、消元法、假定法、逆推法、列举法等。

4、所以分母的arctanx麦克劳林展开时只需展开最低阶无穷小。而分子因为有对c*x 和 d*x的加减运算，所以要展开到x及以上的无穷小，才能确定精度！未完待续。

5、求这一道高数题的第一步，用高数求极限的洛必达法则。而最后一步，求这一道高数题时，用的是高数中无穷大的导数是无穷小，即极限等于0。具体的求求这一道高数题的详细步骤及说明见上。

高数解题,要解题步骤

1、。解：复合函数y=3ln(1-x)；定义域：由1-x0，得定义域为-1x1；2。

2、当极限式最外层是一个0/0型分式时，将其分子分母都完全泰勒展开，则其结果仅由最低阶无穷小决定！因为低阶无穷小±高阶无穷小=低阶无穷小，高阶无穷小在比值中完全不影响结果。

3、首先，计算待证明极限的表达式与极限值之差的绝对值，即xn-2/3的绝对值表达式；如果假设有一个足够小的E，总能找到一个N，使计算式在n比这个N大后，前述绝对值的表达式一定小于E。得到极限值的证明。

4、你用哪个版本的高数字？你在说什么隐函数定理？图2。要学习多元函数的微分，就要结合一元函数的微分来学习。通过这种方式，可以更容易地理解一些相似的定理和命题。

高数求详细解题步骤

1、。解：复合函数y=3ln(1-x)；定义域：由1-x0，得定义域为-1x1；2。

2、求解的第一步：按隐函数存在定理，求出高数此题的两个偏导数。求解的第二步：将已知点代入第一步求出的两个偏导数。求解的第三步：根据全微分dz=Zxdx+Zydy，就可以求解出此高数题目的全微分了。

3、首先，计算待证明极限的表达式与极限值之差的绝对值，即xn-2/3的绝对值表达式；如果假设有一个足够小的E，总能找到一个N，使计算式在n比这个N大后，前述绝对值的表达式一定小于E。得到极限值的证明。

4、对应特征方程：r^2+25=0，解出x1，2=±5i，是虚根，则y=e^ax(c1coswx+c2sinwx)，由虚根知a=0，w=5，代入得y=c1cos5x+c2sin5x，把两个x=0的方程值代入求得c1，c2即可。

5、所以题目中原式=F(x)-F(0)=∫(x，0)costdt 那么该函数求导 =(F(x)-F(0))而F(0)是一个常数，所以它的导数=0 =F(x)-0 =F(x)前面假设F(x)是不定积分。

6、关于求这道高数题，其解题的过程见下图。这道高数题解题原理，主要是用极限定义去证明的。解题过程，极限定义，不定式放缩，然后再用极限定义。具体的这道高数题解题证明的详细过程见下。

高数。求解答过程,谢谢。

1、高数问题解答过程，见上图。这道高数问题的第一题，第一步用等价，等价后代入，即得。高数问题的第二题，第一步用有理化，然后化简，再代入即得。具体的求高数问题解答过程见上。

2、令1+cosθ=3cosθ， 求得 θ= π/3 作出图形，代求面积关于θ=0对称，所以求一半再乘以2就可以了。代求面积分为两部分求。以上，请采纳。

3、那我到底N取多少呢？取它们之中最大的2K，n2K自然也大于2K-1，所以一下子奇数偶数都满足了。解答上就是把上面的思考过程都没写，最后直接取N=2K再验证，我说的是如何找出N=2K的过程。

4、即此向量a在xoy平面上，起点在原点，模为2，且与∠xoy的角平方线重合。

5、椭圆抛物面是指当z取任意一个定值时，x，y组成的方程为一个椭圆；而当x或y取定值时，x，z或y，z组成的方程为抛物线。方程为[(x-p)^2]/a^2+[(y-q)^2]/b^2+z/c=1，其顶点为（p，q，c）。

6、明朗化，在减少多项式项数，降低多项式结构复杂程度等方面有独到作用。解积分题一般有两类换元法，一种不利用三角函数，一种是利用三角函数。

到此，以上就是小编对于高数解题过程分析的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。