本篇目录：

• 1、DFT的计算步骤是什么?
• 2、傅里叶变换中相位频谱怎么求?
• 3、声表滤波器的频谱怎么算
• 4、时域乘积频谱系数怎么算
• 5、用傅里叶变换的微分及积分特性求下图信号的频谱,求详细过程,谢谢
• 6、信号与系统单边指数信号频谱函数计算

DFT的计算步骤是什么?

1、DFT标准算法——通过相关性计算 相关性算法成立的条件是基本函数正交。

2、DFT的运算为：式中 由这种方法计算DFT对于 的每个K值，需要进行4N次实数相乘和（4N-2）次相加，对于N个k值，共需4N*4N次实数相乘和（4N-2)(4N-2）次实数相加。

3、可以看到，完成上式N＝4的FFT计算（表8－1）需要N·（m－1）/2＝2次复数乘法和N·m＝8次复数加法，比N＝4的DFT算法的N2＝16次复数乘法和N·（N－1）＝12次复数加法要少得多。

傅里叶变换中相位频谱怎么求?

1、傅里叶变换后的序列为F(w)=|F(w)|*e(j*f(w))。其中|F(w)|与w的关系就是幅度谱，f(w)与w的关系就是相位谱。

2、周期函数：最终傅里叶级数函数的单边图、双边图、相位谱、幅度谱，如下图所示：幅度谱，也就是频谱，从构成这个波形的各个频率分量的侧面看过去，每一个频率分量都会在侧面投影成一个高度为幅值的线段，构成频谱。

3、看指数形式傅里叶就知道Fn是什么了。为第n个虚指数频率分量[频率=n倍基波频率]的复振幅，包含幅度和相位。就是|Fn|、ψn；Fn是复数的时候，|Fn|=[实部平方+虚部平方]再开方，ψn=[虚部除以实部]再求反正切。

4、，为了能既方便又明白地表示一个信号在不同频率下的幅值和相位，可以采用成为频谱图的表示方法。2，在傅里叶分析中，把各个分量的幅度|Fn|或 Cn 随着频率nω1的变化称为信号的幅度谱。

声表滤波器的频谱怎么算

1、计算公式为：F (cutoff) = 1 / (2πRC)。最基础的滤波器是由电阻和电容构建的RC滤波器，有低通和高通滤波器之分，RC滤波器的截止频率的计算公式为：F (cutoff) = 1 / (2πRC)。

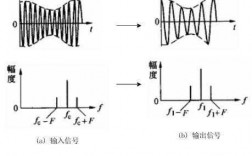
2、将低通滤波器和高通滤波器串联，即可以组成带通滤波器，设前者的截止频率为f1，后者的截止频率为f2，且f2f1，所以通频带（f1-f2）。

3、展开全部 一：一阶 低通滤波器 截止频率 公式为 1/RC和1/(2*Pi*R*C)两个公式是一样的，前者单位是弧度/秒，后者是Hz。

时域乘积频谱系数怎么算

时域卷积可以转为频谱乘积 由于是矩阵，所以需要进行二维傅里叶变换，或者二维离散傅里叶变换，或者二维快速傅里叶变换。

对于频谱很宽的信号，为防止时域采样后产生‘频谱混叠’，一般用前置滤波器滤除幅度较小的高频成分，使信号的贷款小于折叠频率；同样对于持续时间很长的信号，采样点数太多也会导致存储和计算困难，一般也是截取有限点进行计算。

任意函数与简谐信号的时域乘积，其频谱特点：理论中的正弦信号是无限长连续信号，而matlab，参与运算的信号只是截取了其中1个周期或多个周期的信号，就变成 了有限长信号了；无限长信号和有限长信号的傅里叶变换是不一样的。

已知质量m=10kg，弹簧系数k=1000N/m，阻尼c=40Ns/m。且质量块的初始位移x(0)=0.02m，其初始速度x(0)=0m/s。

调制在时域上表现为两个信号相乘，在频域上是频谱的线性搬移。解调的在时域上也是两个的乘积，而在频域上则是将高频的信号搬回到低频段来。

h[n] = DFT{h[m]} = \sum_l g_l*\exp(-j2pi*l*n/N)。每个子载波上的频域信道h[n]是时域tap上的信道{g_l}的线性组合，线性组合的系数随着n的变化而变化。

用傅里叶变换的微分及积分特性求下图信号的频谱,求详细过程,谢谢

1、因为f(t)=g(t-1)，根据位移性质，f(t)的傅里叶变换F（w)=e^(-jw)*G(w)=-e^(-jw)*(πδ（w)-1/jw)，即频谱。

2、步骤1：先把f(t)的函数形式表示出来：f(t)={ 0， t=-2；t， -2t=-1；1， -1t=1；- t- 2， 1t=2；0， 2t；步骤2： 再根据傅里叶变换的定义，把t分段即可计算出傅里叶变换所要的那个积分。

3、正弦信号 c(t) = sin(wt) 的频谱可以通过傅里叶变换来求得。傅里叶变换将信号从时域转换到频域，可以得到信号在不同频率下的幅度和相位信息。

4、符号函数的定义是：sgn(t)=1， 当 t=0； =-1 当 t0.它是一奇函数。奇函数的傅里叶变换是纯虚的， 等于2(1/jw) 。

5、(sin100t/50t)=2Sa(100t)，其傅里叶变换为门宽200的门函数，所以占用频带为100rad/s，乘以cos1000t后，占有的频带范围为900~1100rad/s的范围内。

6、具体回答如图：将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。

信号与系统单边指数信号频谱函数计算

1、指数函数（单边）f(t)=e-atu(t) F(w)=1，实际上是一个低通滤波器a+jw。单位冲激函数F（w）=1，频带无限宽，是一个均匀谱。

2、f(t)=(I+sinω0t)sinω0t =I*sinω0t+sinω0t*sinω0t =I*sinω0t+(1-cos2ω0t)/2 因此，信号含有ω0和2ω0的频率成分 幅值分别为√2I/2和√2/4。

3、其中，C(f) 是频率为 f 的信号在频域的复数表示，i 是虚数单位，* 表示复数的乘法，exp(-2πift) 是复指数函数。

4、如图。补充：因为sgn(t)是符号函数，所以sgn(2t-4)=sgn(t-2)，这样直接用傅里叶变换的时移性质就能得到结果。当然，结果肯定和图上的一样。20200907二次补充：看到评论提出了新的问题。

5、表示直流信号就是一个频率等于零的信号。与此相反，冲激函数的频谱函数等于常数，表示冲激函数含有无限多个、频率无限密集的正弦成分。同样的，单个正弦波的频谱函数就是频域中位于该正弦波频率处的一对冲激函数。

6、先求2Sa(2t)的 频谱函数--这个可以查表，或记得住[或由门信号的频谱和对称互易特性求出]，再用频谱搬移即可，即左搬右搬，幅度减半即可。

到此，以上就是小编对于频谱的计算公式的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。