本篇目录:
方差的简化公式是怎么得到的?
1、方差的简化公式是根据样本数据的平均值和每个数据点与平均值的差的平方来计算的。设样本数据为 x, x, ..., x,样本平均值为 x。
2、方差描述随机变量对于数学期望的偏离程度。单个偏离是消除符号影响方差即偏离平方的均值,记为D(X):直接计算公式分离散型和连续型,具体为:这里 是一个数。推导另一种计算公式得到:“方差等于平方的均值减去均值的平方”。
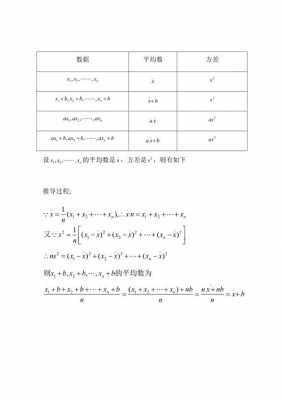
3、(X-X拔)^2 ),我这里是E((X-EX)^2 ).还想强调的是:均值EX在统计学中的意义是数据的中心,那么X-EX就是离开中心的距离,称离差,因此方差可以简记为“离差平方的平均值”,再简单地记就是:方差是差方的均值。
方差公式证明
如果一组数据的方差越小,那么就证明该组数据的稳定性较高。常见方差公式:(1)设c是常数,则D(c)=0。(2)设X是随机变量,c是常数,则有D(cX)=(c)D(X)。
先证明E(x)=a,然后按定义展开E(x^2)=a^2+a 因为D(x)=E(x^2)-[E(x)]^2,得证。
=E{X^2-2XE(X)+[E(X)]^2} =E(X^2)-2[E(X)]^2+[E(X)]^2 数学期望为设X是一个随机变量,若E{[X-E(X)]^2}存在,则称E{[X-E(X)]^2}为X的方差,记为D(X),Var(X)或DX。
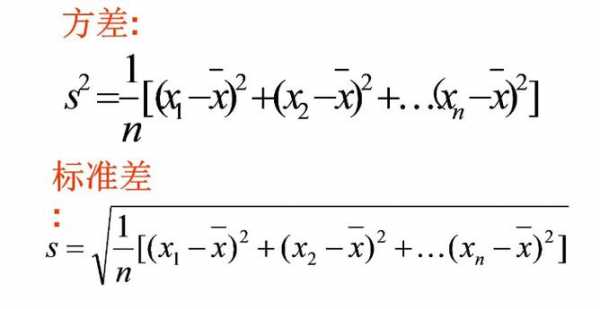
如果X~P(a)那么E(x)=D(x)=a 先证明E(x)=a 然后按定义展开E(x^2)=a^2+a 因为D(x)=E(x^2)-[E(x)]^2,得证。泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
几何分布的期望与方差公式怎么推导
1、几何分布,P(X=n)=(1p)^(n1)p,随着n增大呈等比级数变化,等比级数又称几何级数。这可能和以前几何学中无限分割图形得到的级数有关。
2、超几何分布的期望和方差公式:E(X)=(n*M)/N[其中x是样本数,n为样本容量,M为样本总数,N为总体中的个体总数],求出均值,这就是超几何分布的数学期望值。
3、几何分布的期望和方差公式分别是E(n)等于1/p、E(m)等于(1-p)/p,几何分布是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。

4、方差公式是V(X)=X1^2*P1+X2^2*P2+...Xn^2*Pn-a^2[这里设a为期望值]。超几何分布是统计学上一种离散概率分布。
5、数学期望和方差公式为:EX=npDX=np(1-p)、EX=1/PDX=p^2/q、DX=E(X)^2-(EX)^2。对于2项分布(例子:在n次试验中有K次成功,每次成功概率为P,它的分布列求数学期望和方差)有EX=npDX=np(1-p)。
正态分布的均值与方差怎么算?
1、惹X~N(p,k^2)的正态分布,则Z=(X-p)/k~N(0,1)的标准正态分布,即统计量减期望值后除以方差。
2、正态分布的方差是σ^2。 如果已知正态分布的数据样本,那么可以使用样本均值和样本方差来近似估计正态分布的平均值和方差。
3、具体而言,如果X和Y是两个独立的正态分布变量,其均值分别为μ1和μ2,方差分别为σ1和σ2,则它们的和Z=X+Y 服从均值为μ1+μ2,方差为σ1+σ2 的正态分布。
4、设正态分布概率密度函数是f(x)=[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]其实就是均值是u,方差是t^2。
如何计算方差和均值?
1、E(χ^2)=n D(χ^2)=2n E(均值)=E(χ^2) D(均值)=2n/n=2。它们的均值等于他们相加除以十,根据E(ax+by)=aE(x)+bE(y),V(ax+by)=a2V(x)+b2V(y),样本均值的期望和他们的期望一样,也就是N。
2、方差的计算公式是s2={(x1-m)2+(x2-m)2+(x3-m)2+…+(xn-m)2}/n,公式中M为数据的平均数,n为数据的个数,s2为方差。文字表示为方差等于各个数据与其算术平均数的离差平方和的平均数。
3、: 均方根值 均方根值,用RMS(root mean square),既均方值的开根号 5 :均方差 均方差(mean square error),用MSE表示。
4、均值和方差都是通过对数据进行计算和处理得出的统计量。需要先对数据进行收集和整理,然后进行计算和分析。都可以用于评估数据的质量和可靠性:均值和方差都可以用于评估数据的质量和可靠性。
5、有n个数,先求平均值Ex,则方差var(n)=/n。“方差”(variance)这一词语率先由罗纳德·费雪(Ronald Fisher)在其论文《The Correlation Between Relatives on the Supposition of Mendelian Inheritance》中提出。
6、其实就是均值是u,方差是t^2。于是:∫e^[-(x-u)^2/2(t^2)]dx=(√2π)t(*)积分区域是从负无穷到正无穷,下面出现的积分也都是这个区域。
方差的基本公式到简易公式的推导
方差 = E[(X - E[X])^2]其中 X 是随机变量,E[X] 表示 X 的期望值。
.设C为常数,则D(C) = 0(常数无波动)。2.D(CX )=C2D(X )(常数平方提取,C为常数,X为随机变量);证:特别地D(-X ) = D(X ), D(-2X ) = 4D(X )(方差无负值)。
方差公式:标准方差公式(1):标准方差公式(2):例如两人的5次测验成绩如下:X:50,100,100,60,50,平均值E(X)=72;Y:73,70,75,72,70平均值E(Y)=72。
由方差的定义可以得到以下常用计算公式:D(X)=E(X^2)-[E(X)]^2 方差的几个重要性质(设一下各个方差均存在)。(1)设c是常数,则D(c)=0。(2)设X是随机变量,c是常数,则有D(cX)=(c^2)D(X)。
到此,以上就是小编对于方差推导公式dx=e的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏