本篇目录：

• 1、椭圆是什么时候传入中国的
• 2、谁有椭圆知识总结
• 3、椭圆的相关知识点是什么?
• 4、椭圆的知识点有哪些?
• 5、椭圆什么时候学
• 6、关于椭圆的知识

椭圆是什么时候传入中国的

1、所以，英国旅行家巴洛在1804年出版的《中国游记》中叙述他在广州的见闻时说：“传入广州的欧洲彩色版画，被复制得十分逼真。” 虽然临仿是清代南方通商口岸油画发展的早期方式，但在此基础上焕发出来的油画创作，奠定了油画在中国南方盛起的基础。

2、哥白尼的太阳中心说、开普勒的椭圆轨道、牛顿的万有引力三者相继传入中国，它们和中土奉为圭臬的“天动地静”、“天圆地方”、“阴阳相感”的传统有天壤之别。这就不能不引起中国人的巨大反响。牛顿学说在中国的传播决不只是影响了学术界，唤醒了人们对于科学真理的认识。

3、葡萄是2000多年前传入中国的，在汉朝。《本草纲目》：“葡萄，汉书作 蒲桃，可以入酺，饮人则陶然而醉，故有是名。其圆者名草龙珠，长者名马乳葡萄，白者名水晶葡萄，黑者名紫葡萄。汉书言张骞使西域还，始得此种。而《神农本草经》已有葡萄，则汉前陇西旧有，但未入关耳。

4、拨弦类弦鸣乐器。木制，音箱呈半梨形，上装四弦，原先是用丝线，现多用钢丝、钢绳、尼龙制成。颈与面板上设用以确定音位的“相”和“品”。演奏时竖抱，左手按弦，右手五指弹奏，是可独奏、伴奏、重奏、合奏的重要民族乐器。筝：又称古筝、秦筝，中国古老的传统弹拨乐器。

5、葡萄的品种繁多，有圆形的草龙珠、长形的马乳葡萄、白色的水晶葡萄以及黑色的紫葡萄等。据《汉书》记载，葡萄是在张骞出使西域后才传入中国的，但《神农本草经》中已有葡萄的记载，说明葡萄在汉朝之前就已经存在于陇西地区。 葡萄是一种营养价值极高的水果，其浆果多为圆形或椭圆形，色泽多样。

6、穗形总状花序，小穗含4-10小花，小穗轴节间长1-5毫米，平滑无毛；颖较宽大，与其小穗近等长，外稃椭圆形至卵形，成熟时肿胀，基盘微小芒近外稃顶端伸出，长1-2厘米，粗糙；内稃约等长于外稃，颖果为其宽的2-3倍。花果期6-7月。

谁有椭圆知识总结

椭圆的相关知识点如下：椭圆的标准方程：当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。其猛冲中a^2-c^2=b^2。

椭圆的相关知识点如下：离心率越小越接近于圆，越大则椭圆就越扁。当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。椭圆是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。

椭圆的几何性质知识点有：范围、对称性、顶点、离心率等。范围：要注意方程与函数的区别与联系；与椭圆有关的求最值是变量的取值范围；作椭圆的草图。

椭圆的标准方程：当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)；当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)；其中a^2-c^2=b^2。

高二椭圆的相关知识点如下：在平面内到两定点FF的距离的和等于常数（大于IFF）的点的轨迹（或集合）叫椭圆，这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。集合P={M/MF1+MF2=2a}，FF2=2c，其中a0，c0，且a，c为常数：（1）若ac，则集合P为椭圆。

椭圆的相关知识点是什么?

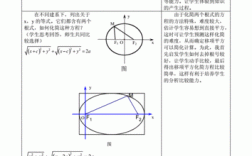
椭圆的相关知识点包括：定义、标准方程、几何性质以及椭圆的应用。 定义：椭圆是一种平面上的几何图形，定义为平面内到两定点距离之和等于常数的点的轨迹。这两定点称为椭圆的焦点，它们到椭圆上任一点的距离之和恒等于椭圆的长轴长度。其中两焦点的距离用公式表示是F = √。

椭圆的几何性质知识点有：范围、对称性、顶点、离心率等。范围：要注意方程与函数的区别与联系；与椭圆有关的求最值是变量的取值范围；作椭圆的草图。

椭圆是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a|F1F2|）。椭圆是圆锥曲线的一种，即圆锥与平面的截线。椭圆的周长等于特定的正弦曲线在一个周期内的长度。

高二椭圆的相关知识点如下：在平面内到两定点FF的距离的和等于常数（大于IFF）的点的轨迹（或集合）叫椭圆，这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。集合P={M/MF1+MF2=2a}，FF2=2c，其中a0，c0，且a，c为常数：（1）若ac，则集合P为椭圆。

椭圆的定义：椭圆是平面上距离到两个定点之和等于常数的点的集合。这两个定点称为焦点，常数称为离心率。 椭圆的性质：- 长轴与短轴：椭圆的两个焦点之间的距离称为长轴的长度，过椭圆中心并且垂直于长轴的直线称为短轴。

椭圆的知识点有哪些?

椭圆的相关知识点包括：定义、标准方程、几何性质以及椭圆的应用。 定义：椭圆是一种平面上的几何图形，定义为平面内到两定点距离之和等于常数的点的轨迹。这两定点称为椭圆的焦点，它们到椭圆上任一点的距离之和恒等于椭圆的长轴长度。其中两焦点的距离用公式表示是F = √。

椭圆是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a|F1F2|）。椭圆是圆锥曲线的一种，即圆锥与平面的截线。椭圆的周长等于特定的正弦曲线在一个周期内的长度。

椭圆的几何性质知识点有：范围、对称性、顶点、离心率等。范围：要注意方程与函数的区别与联系；与椭圆有关的求最值是变量的取值范围；作椭圆的草图。

高二椭圆的相关知识点如下：在平面内到两定点FF的距离的和等于常数（大于IFF）的点的轨迹（或集合）叫椭圆，这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。集合P={M/MF1+MF2=2a}，FF2=2c，其中a0，c0，且a，c为常数：（1）若ac，则集合P为椭圆。

椭圆什么时候学

椭圆的相关知识是在高二数学的选修一中学到的。椭圆的相关知识是在高二数学的选修一中学到的。椭圆的标准方程是描述椭圆上的点到两个焦点的距离之和等于一个常数的数学模型，这是椭圆的基本性质之一。椭圆的几何性质还包括焦点、焦距等概念，以及椭圆的离心率等相关计算。

人教版的教材，数学学完必修二之后一般是学必修三，学完必修一，接下来到“离散数学”，然后必修二，到“概率论与数理统计”，必修三，“工程数学”，“统计学”，必修四。椭圆在选修2-1第二章圆锥曲线与方程中会学习到。

椭圆积分是数学中的一种积分，通常在高中数学中学习。椭圆积分最初出现于椭圆的弧长有关的问题中。Guilio Fagnano和欧拉是最早的研究者。通常，椭圆积分不能用基本函数表达。这个一般规则的例外出现在P有重根的时候，或者是R(x，y)没有y的奇次项的时候。

关于椭圆的知识

椭圆的几何性质知识点有：范围、对称性、顶点、离心率等。范围：要注意方程与函数的区别与联系；与椭圆有关的求最值是变量的取值范围；作椭圆的草图。

椭圆的焦距是椭圆的第一定义：其中两定点F、F叫做椭圆的焦点，两焦点的距离│FF│=2c。焦距=2cc2=a2-b2。椭圆（Ellipse）是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a|F1F2|）。

高二椭圆的相关知识点如下：在平面内到两定点FF的距离的和等于常数（大于IFF）的点的轨迹（或集合）叫椭圆，这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。集合P={M/MF1+MF2=2a}，FF2=2c，其中a0，c0，且a，c为常数：（1）若ac，则集合P为椭圆。

到此，以上就是小编对于椭圆概念知识形成过程是什么的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。