本篇目录:
10道大一高数小题,请写出演算过程。
假设长方体的长为x,宽为y,高为z,那么表面积为6。根据长方体表面积公式,我们可以写出:2(xy + xz + yz) = 6 要使长方体的体积V = xyz最大,我们需要使用拉格朗日乘数法来解决这个约束优化问题。
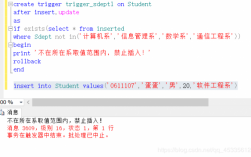
n+1)时,数列 ▏Un▕ 收敛时,数列U不收敛。因为lim(x→∞)Un=a,任取δ0,存在N。使nN,|Xn - a|δ 当nN时,||Xn|-|a||=|Xn - a|δ,得证。应该就是这样吧,忘的太厉害了小叶子。

把f(x)求出来,就是求那个极限,显然要对X讨论吗,|x|1时,lim x^2n=0,所以f(x)=-1;|x|1时,把分子分母除x^2n再求极限,得到f(x)=1;|x|=1时,f(x)=0。
这几道题都符合1的无穷大次方这一情形,因此可以用洛必达法则来求。
罗尔定理:f(0)=f(1)=f(2)=f(3)=0 所以,根据罗尔定理,在(0,1)、(1,2)、(2,3)内 方程 f (x)=0各有一根,又 f (x) 是三次多项式,所以,方程 f (x)=0最多有3个实根。
高数如何推翻1等于0.9循环?
高数没有推翻1等于0.9循环。方法一:我们知道1/3等于0.33333…2/3等于0.66666…所以1/3+2/3必须等于0.3333…+0.6666…两边相加,结果1=0.999。
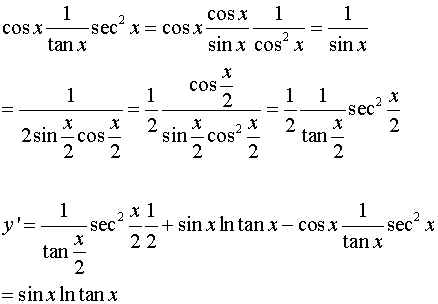
在分数1/3化小数时做除法,1除以3,下一位商3。33得9后余1,所以永远除不尽。这时1/3是等于0.3循环的。但是高数里的0.3循环是由数列求和的级数得到的。
那么:0.9 (9循环)=0.9+0.09+0.009+...+0.9*0.1的(n-1)次方=0.9*(1-0.1的n次方)/(1-0.1)=1-0.1的n次方。所以当n趋向于无穷大时0.1的n次方趋向于0 所以0.9 (9循环)=1。
数学上0.9(9循环)和1是相等的值。可以令x=0.9(9循环),则10x=9(9循环),10x-x则可以消去小数部分,即9x=9,得x=1。
求高数题目解法,求写出必要的演算和解答过程,高分重谢!!
归类小结是一个重要方法。高等数学归类方法可按内容和方法两部分小结,以代表性问题为例辅以说明。
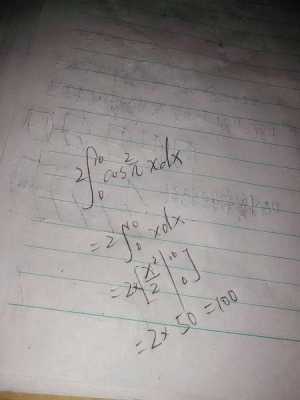
求高数大神帮我解一道题 非齐次项 sinx 对应于 e^(ix), 故特解形式是 y = x(Asinx+Bsinx); 非齐次项 cos2x 对应的特解是 Ccos2x. 故选 B。
)=lim 2/(√(1+1/x+1/x^2)+√(1-1/x+1/x^2)) (分子分母同时除以x)x-+∞时,1/x,1/x^2-0 故原式=2/(1+1)=1 如果认为讲解不够清楚,请追问。
题选B,上述表达式中,1可以直接并入常数C;10题选A。
如何学习高等数学逻辑?
保持好奇心:对未知的事物保持好奇心,是培养逻辑思维的重要动力。只有对未知的事物充满好奇,你才会有动力去探索和学习。培养耐心:数学思维的培养需要时间和耐心。你需要不断地学习和实践,才能逐渐提高你的逻辑思维能力。
学习高等数学需要建立以下几种逻辑思维:抽象思维:高等数学中的概念和理论往往比初等数学更为抽象,因此需要具备较强的抽象思维能力。这包括从具体问题中提炼出一般规律,以及将一般规律应用于具体问题的能力。
培养抽象思维能力:高等数学要求学生从具体问题中抽象出一般性的规律和定理,这有助于培养学生的抽象思维能力。
要学好基础,对三角函数,几何,代数,概率等高中课程要精通,最起码要熟练掌握基本的理论,而高等数学就是进一步深入学习这些东西,只有把这些基础课程弄明白才能学好高等数学。
学高等数学,一定不能太死板。要学会举一反三,同样的考核目的,可以有不同的考核形式。在学习的过程中,一定要多用心,多去思考。
书本习题做完以后就是上机编程学习了,这个是你对于高等数学公式的逻辑理解的训练,你可使用R语言或者matlab语言来把你的定理试着编成计算机语言,这个过程很艰难,但是对于你的逻辑训练很有帮助,能让你更好的理解公式。
到此,以上就是小编对于高数演算过程图片的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏