本篇目录:
独立增量过程是什么
区别如下:独立增量过程,状态离散的平稳独立增量过程是一类特殊的马尔可夫过程。正交增量过程(process with orthogonal increments)是一种随机过程。指在不相交区间上的增量不相关的随机过程。
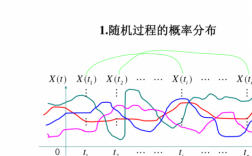
独立增量过程是指在不同时间点上的增量是相互独立的随机变量。也就是说,对于任意时点t1t..tn和正整数k1k..km,随机变量X(t2)-X(t1),X(t3)-X(t2),...,X(tk)-X(tk-1)是相互独立的。

维纳过程是一个重要的独立增量过程,也称作布朗运动过程。数学中,维纳过程是一种连续时间随机过程,得名于诺伯特·维纳。由于与物理学中的布朗运动有密切关系,也常被称为“布朗运动过程”或简称为布朗运动。
如何证明独立增量过程一定是马尔可夫随机过程
马尔可夫过程本身就是X(n+1)仅与X(n)有关的一类过程阿,这是定义。
是独立随机变量序列,故为马尔可夫过程,其状态集E={0,±1,±2,…},所以X(n)是马尔可夫链。
马尔科夫过程的局限性 一个实际的问题是语音识别,我们听到的声音是来自于声带、喉咙大小、舌头位置以及其他一些东西的组合结果。

其基本性质为:布朗运动W(t)是期望为0方差为t(时间)的正态随机变量。对于任意的r小于等于s,W(t)-W(s)独立于的W(r),且是期望为0方差为t-s的正态随机变量。可以证明布朗运动是马尔可夫过程、鞅过程和伊藤过程。
年前后,伊藤清建立的随机微分方程的理论,为马尔可夫过程的研究开辟了新的道路。1954年前后,W.费勒将半群方法引入马尔可夫过程的研究。流形上的马尔可夫过程、马尔可夫向量场等都是正待深入研究的领域。
证明一个随机过程是宽平稳过程或者独立增量过程:平稳分为严平稳和宽平稳,严平稳是指,任取x1,x2,xn,任取k,p(x1,x2,xn)=p(x1-k,x2-k,xn-k)。
如何证明一个随机过程是宽平稳过程或者独立增量过程?
注:二阶矩过程定义:如果随机过程{X(t),t∈T}对每一个t∈T,二阶矩E[X(t)·X(t)]都存在,那么称它为二阶矩过程。

平稳独立增量过程不是宽平稳过程。平稳独立增量过程是指随机过程在不间区间上的增量是独立的,有相同的分布。这意味该过程的统计特性在时间上是不变的。
现在来证明伯努利过程不是独立增量过程。假设我们选择三个时间点t1t2t3,并考虑伯努利过程在这些时间点的状态。
维纳过程是独立增量过程。知道了这一点,以下是计算问题。--- {W(t), t≥0}, σt, 是一个维纳过程. X(t)=W(t)-aW(t-h), t≥0, h0 是常数. 求:X(t)的一维概率密度分布函数。
例如,白噪声(AWGN)就是平稳过程,铙钹的敲击声是非平稳的。尽管铙钹的敲击声基本上是白噪声,但是这个噪声随着时间变化:在敲击前是安静的,在敲击后声音逐渐减弱。
维纳原理在在运动中哪些方面体现?
1、维纳过程又称布朗运动,它具有如下特点:⑴它是一个Markov过程。因此该过程的当前值就是做出其未来预测中所需的全部信息。⑵维纳过程具有独立增量。
2、维纳过程和物理学中的布朗运动有密切关系。布朗运动是指悬浮在液体中的花粉微小颗粒所进行的无休止随机运动。维纳运动也可以描述由福克-普朗克方程和郎之万方程确定的其他随机运动。
3、Brown 运动是特殊的 Gauss 过程 关于 Brown 运动的积分 积分 公式 随机分析中的链式法则the chain rule。
到此,以上就是小编对于随机过程平稳独立增量函数的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏