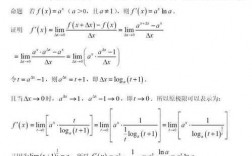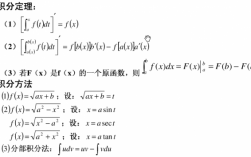本篇目录:
三角函数反正弦、余弦、正割、余切怎么求导?
1、反三角函数的求导公式:反正弦函数求导:(arcsinx)=1/√(1-x^2);反余弦函数求导:(arccosx)=-1/√(1-x^2);反正切函数求导:(arctanx)=1/(1+x^2);反余切函数求导:(arccotx)=-1/(1+x^2)。
2、反余切函数的求导 (arccotx)=-1/(1+x^2)为限制反三角函数为单值函数,将反正弦函数的值y限在-π/2≤y≤π/2,将y作为反正弦函数的主值,记为y=arcsinx。相应地。
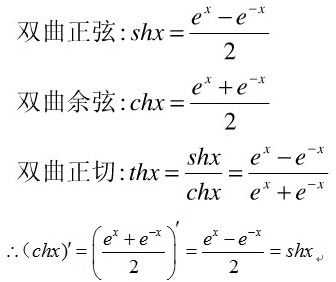
3、正弦函数的导数公式:(sinx)=cosx。即正弦函数的导数等于余弦函数。余弦函数的导数公式:(cosx)=-sinx。即余弦函数的导数等于正弦函数的相反数。正切函数的导数公式:(tanx)=sec^2x。
4、反三角函数 反三角函数是一种基本初等函数。
5、反双曲正弦函数的导数可以表示为d/dxarcsinh(x)=1/√[x+1]。定义:我们知道,三角函数分为sin(正弦)、cos(余弦)、tan(正切)、cot(余切)、sec(正割)、csc(余割)六种。而双曲函数也如此。
三角函数的导数推导过程
1、三角函数求导公式推导如下:设f(x)=sinx;(f(x+dx)-f(x))/dx=(sin(x+dx)-sinx)/dx=(sinxcosdx+sindxcosx-sinx)/dx,因为dx趋近于0,cosdx趋近于1,(f(x+dx)-f(x))/dx=sindxcosx/dx。

2、sinx的导数是cosx(其中x为变量),sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
3、首先,我们来计算正弦函数sin(x)的导数。
余弦函数的导数怎么求?
1、求导公式表如下:(sinx)=cosx,即正弦的导数是余弦。(cosx)=-sinx,即余弦的导数是正弦的相反数。(tanx)=(secx)^2,即正切的导数是正割的平方。
2、cosx的导数是-sinx。即y=cosx y=-sinx。证明过程:用和差化积公式cos(a) - cos(b) = - 2sin[(a+b)/2]sin[(a-b)/2]。重要极限lim(h-0) sin(h)/h = 1。

3、余弦函数的n阶导数为(cosx)^(n)=ducos(x+n(Pi/2))。当n=2m+1时,等于0。当n=2m时,等于(-1)。所以,cosx=1-x^2/2!+x^4/4!+...+(-1)^m*x^(2m)/(2m)!+o(x^(2m))。
4、(cosx)^2-(sinx)^2=1-(sinx)^2-(sinx)^2=1-2(sinx)^2=cos2x。余弦(余弦函数),三角函数的一种。
sinx的导数及推导过程
sinx的导数是cosx(其中x为变量),sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
cscx是sinx的倒数,即cscx=1/sinx。secx是cosx的倒数,即secx=1/cosx、三角函数是基本初等函数之一,是以角度为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
sinx求导推导过程如下:sinx是一个三角函数,它的值在-1和1之间波动,其周期为2π。对于任意实数x,sinx的导数可以用微积分中的求导法则来求解。根据求导法则,对于函数f(x)=sinx,我们可以将其表示为f(x)=cosx。
sinx是正弦函数,而cosx是余弦函数,两者导数不同,sinx的导数是cosx,而cosx的导数是 -sinx,这是因为两个函数的不同的单调区间造成的。
到此,以上就是小编对于求余弦的求导过程的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏