本篇目录：

• 1、圆锥体积公式,推导过程
• 2、圆锥的面积推到过程怎么推导??急需!!
• 3、圆锥的体积公式如何推导,详细过程。
• 4、圆锥的侧面积公式推导过程,为什么要乘上1/2
• 5、圆锥体积推导过程

圆锥体积公式,推导过程

一个圆锥的体积等于与它等底等高的圆柱的体积的1/3，根据圆柱体积公式V=Sh(V=rrπh)，得出圆锥体积公式：圆锥V=1/3Sh。S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。证明：把圆锥沿高分成k分，每份高h/k。

圆锥体的体积由圆柱推导而来。设 h为圆台的高， r和R为棱台的上下底面半径， V 为圆台的体积。

根据圆柱体积公式V=Sh（V=rrπh），得出圆锥体积公式：圆锥 V=1/3Sh S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。

所以V=1/3πr/H*H-1/3πr/H*0=1/3πrH-0=1/3πrH所以，圆锥体积=1/3乘底面积乘高。

圆柱的体积公式是V=Sh 那么与它等底等高的圆锥的体积是多少呢？把与它等底等高的圆锥装满水，倒进圆锥体里，你可以发现倒3次才能倒满圆柱。

圆锥的面积推到过程怎么推导??急需!!

1、圆锥的表面积=底面积+侧面积，公式推导为：S表=S侧+S底=π×r×r+π×r×L=πr×（r+L）；其中r表示地面半径，L表示圆锥的母线，π为圆周率。

2、把圆锥展开，可以得到一个圆和一个扇形。这是计算的思路。公式为：πr+πrL。（其中r为半径，π为圆周率，通常取14。L为母线长）。S底=πr。

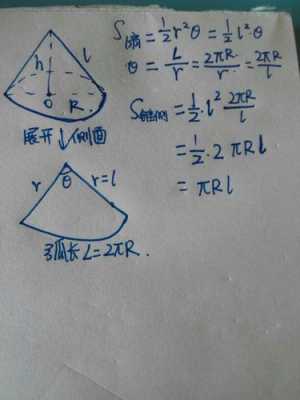
3、先了解圆锥母线，圆锥母线可以这么理解：从圆锥顶点到底面圆上任意一点的线段叫圆锥母线，用字母l表示。沿着圆锥母线将圆锥侧面减掉，并展开，得到一个扇形。

4、把圆锥侧表面展开，应该是一个扇形，这个扇形的半径就是L，扇形的弧长就是底圆的周长，为：2Πr。以L为半径的大圆的周长为：2ΠL。面积为：ΠL=Π（h+r)。

5、将圆锥沿着母线剪开，得到圆锥的侧面展开图——扇形，可利用扇形面积公式计算。圆锥的侧面展开图是一个扇形，其半径等于圆锥的母线长，弧长等于圆锥的底面周长。

圆锥的体积公式如何推导,详细过程。

一个圆锥的体积等于与它等底等高的圆柱的体积的1/3，根据圆柱体积公式V=Sh(V=rrπh)，得出圆锥体积公式：圆锥V=1/3Sh。S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。证明：把圆锥沿高分成k分，每份高h/k。

用极限法可以推导： V＝1/3Sh（V＝1/3SH）S是底面积，h是高，r是底面半径。设圆锥高为h，底部半径为r，把圆锥等分为k份，每份看做一个小圆柱。则第n份圆柱的高为h/k， 半径为n*r/k。

根据圆柱体积公式V=Sh（V=rrπh），得出圆锥体积公式：圆锥 V=1/3Sh S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。

圆锥的侧面积公式推导过程,为什么要乘上1/2

圆锥的侧面是一个扇形，所以圆锥侧面积公式和扇形面积公式是一样的，扇形的面积公式为S=(1/2)lr。下面解释1/2是什么东西了。 通常我们计算扇形的面积时是套用三角形的计算模式的，就是1/2的底乘以高。

圆锥侧面积的公式×2πr×l表示圆锥底面的半周长与母线之积。理由：∵圆锥侧面展开是一个扇形，扇形的面积=nπR/360=nπR/180·1/2R=L·1/2R=1/2LR （L是扇形的弧长，L=nπR/180。

圆锥侧面积公式推导过程如下：推导过程 首先，我们知道圆的周长公式为C=2πr，其中r是圆的半径。当这个圆被一条母线和一个顶点截割成扇形时，扇形的弧长就是圆的周长，即扇形的弧长为C=2πr。

原因：根据扇形面积公式：S=1/2*弧长*半径，S侧=1/2*2πr*L=πr*L 圆锥的侧面积：将圆锥的侧面沿母线展开，是一个扇形，这个扇形的弧长等于圆锥底面的周长，而扇形的半径等于圆锥的母线的长。

这个公式的推导过程如下：圆锥的侧面可以展开成一个扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长。因此，圆锥侧面积可以用扇形的面积来表示。

圆锥的侧面积公式推导过程：设圆锥的底面半径为r，高为h，母线长为l（l^=r^+h^），圆锥侧面展开图是一个扇形，半径为l，弧长为2πr，圆锥侧面积=(1/2)(2πr)l=πrl。

圆锥体积推导过程

圆锥体的体积由圆柱推导而来。设 h为圆台的高， r和R为棱台的上下底面半径， V 为圆台的体积。

推导过程如下：三棱锥2的底ΔABA’、ΔB’A’B的面积相等，高也相等（顶点都是C）。三棱锥3的底ΔB’CB’、ΔC’B’C的面积相等，高也相等.（顶点都是A’）。∴V1=V2=V3=1/3V三棱柱 。∵V棱柱Sh 。

根据圆柱体积公式V=Sh（V=rrπh），得出圆锥体积公式：圆锥 V=1/3Sh S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。

圆锥体积的推导过程可以追溯到古希腊数学家阿基米德。他通过实验和几何方法证明了圆锥的体积公式，即V=1/3πrh，其中r为底面半径，h为圆锥的高。

你好：圆锥的体积是这样推导出的 其实很简单。

所以V=1/3πr/H*H-1/3πr/H*0=1/3πrH-0=1/3πrH所以，圆锥体积=1/3乘底面积乘高。

到此，以上就是小编对于圆锥的公式推导的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。