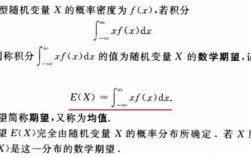本篇目录:
- 1、概率论与数理统计联合分布律
- 2、cov(x1,x2)怎么算
- 3、如何理解协方差的联合分布表?
- 4、如何理解联合概率分布的边缘分布律与边缘分布律?
- 5、数学题,二维离散型随机变数(x,y)的分布律为
- 6、协方差公式Cov(X,Y)=E(((X-E(X))(Y-E(Y)))即Cov(X,Y)=E(XY)-E(X)E...
概率论与数理统计联合分布律
∴ XY=-2,-1,1,2,4这五种情况。
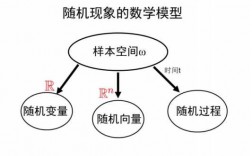
定理1 联合分布函数的性质:二维随机变量也分为离散型和非离散型,如果它取值于平面上的一些离散的点,就称为二维离散型随机变量。下面两图分别给出二维离散型和连续型随机变量的概率分布。

根据题目给出的概率分布表,P(X = 0, Y = -1) = 1/16,P(X = 0) * P(Y = -1) = (1/2) * (1/8) = 1/16。因此,X 和 Y 是独立的。
cov(x1,x2)怎么算
1、从样本中计算每个变量的平均值。构建一个矩阵,其中每个元素都是变量之间的协方差。矩阵的对角线上是每个变量的方差,而其他元素是两个变量之间的协方差。
2、cov计算公式:Cov(X,Y)=E((X-Ex)(Y-Ey));其中,X和Y表示两组样本数据;Ex和EY分别表示X和和Y的样本均值。知识拓展 协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。
3、Cov(X,Y)=Cov(Y,X);Cov(aX,bY)=abCov(X,Y),(a,b是常数);Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)。由协方差定义,可以看出Cov(X,X)=D(X),Cov(Y,Y)=D(Y)。

4、(3)Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)。由协方差定义,可以看出Cov(X,X)=D(X),Cov(Y,Y)=D(Y)。
如何理解协方差的联合分布表?
核心意义:度量各个维度偏离其均值的程度。协方差的值如果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),结果为负值就说明负相关的,如果为0,也是就是统计上说的“相互独立”。
首先,联合分布是指一组随机变量在一起的出现情况。在概率论中,联合分布是用于描述两个或两个以上的随机变量如何共同变化的概率分布函数。因此,联合分布可以理解为这些变量的联合概率密度函数。
则协方差矩阵为:更进一步:矩阵 其协方差矩阵为 还是有点抽象??那就结合实例来理解,可能更方便一些。假定有下列矩阵:我们来计算一下协方差矩阵。

(5)协方差Cov(X,Y)的度量单位是X的协方差乘以Y的协方差。而取决于协方差的相关性,是一个衡量线性独立的无量纲的数。协方差为0的两个随机变量称为是不相关的。
联合分布函数可以帮助我们求出两个变量之间的关系,如概率密度分布函数,协方差,相关系数等。在求联合分布函数时,需要注意以下几点:首先需要明确两个随机变量 X 和 Y 的取值范围。
如何理解联合概率分布的边缘分布律与边缘分布律?
1、边缘分布律是指在概率论和统计学的多维随机变量中,只包含其中部分变量的概率分布。边缘分布中,我们得到只关于一个变量的概率分布,而不再考虑另一变量的影响,实际上进行了降维操作。
2、边缘密度函数是指边缘分布函数,定义是:如果二维随机变量X,Y的分布函数F{x,y}为已知,那么随机变量x,y的分布函数Fx{x}和Fy{y}分别由F{x,y}求得。则Fx{x}和Fy{y}为分布函数F{x,y}的边缘分布函数。
3、具体回答如图:相同的边缘分布可构成不同的联合分布,这反映出两个分量的结合方式不同,相依程度不同。这种差异在各自的边缘分布中没有表现,因而必须考察其联合分布。
数学题,二维离散型随机变数(x,y)的分布律为
P(X=-1)=0.3,P(X=0)=0.4,P(X=2)=0.3;P(Y=1)=0.5,P(Y=3)=0.5 令;a+1/6+1/12+ +1/6+1/6+1/6+ +1/12+1/6+b=1,得:a+b+1=1,即:a+b=0。
∵X,Y是相互独立,则P(X=度1,Y=2)=P(X=1)·P(Y=2)P(X=1)=1/6+1/9+1/18P(Y=2)=1/9+αP(X=1)·P(Y=2)=(1/6+1/9+1/18)·(1/9+α)解得α=2/9。
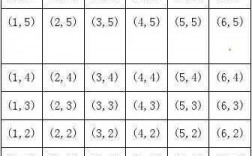
边缘分布律,以x为例,x取0的概率是1/6,取-1概率是1/3+1/12=5/12,取2的概率就是5/12,那么做一个表,第一行是可能的取值0,1,2.第二行把相应概率填进去。
求X的边缘分布律就是把每一纵列相加,把y全部积分,x不积分。0+0.2=0.2 0.2+0.3=0.5 0.2+0.1=0.3 Z的取值一共只有四种情况:-1,0,1,2把这四种情况对应的概率算出就可以。
协方差公式Cov(X,Y)=E(((X-E(X))(Y-E(Y)))即Cov(X,Y)=E(XY)-E(X)E...
定义 E[(X-E(X))(Y-E(Y))]称为随机变量X和Y的协方差,记作COV(X,Y),即COV(X,Y)=E[(X-E(X))(Y-E(Y))]。注意 E[(X-E(X))(Y-E(Y))]= E(XY)-E(X)E(Y) 。
cov(y)代表协方差。 E[(X-E(X))(Y-E(Y))]称为随机变量X和Y的协方差,记作COV(X,Y),即COV(X,Y)=E[(X-E(X))(Y-E(Y))^T]。
用协方差的公式:COV(X,Y)=E[(X-E(X))(Y-E(Y))]=EXY-EX*EY 那么EXY=COV(X,Y)+EX*EYEX,EY,COV(X,Y)都已知,就可以算出。
协方差的计算公式为cov(X,Y)=E[(X-E[X])(Y-E[Y])],这里的E[X]代表变量X的期望。从直观上来看,协方差表示的是两个变量总体误差的期望。
到此,以上就是小编对于联合分布律公式的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏