本篇目录:
- 1、观察图中的两个几何体,它们分别有几个面?是平面还是曲面?面与面相交的...
- 2、关于画法几何里平面与平面的交线画法问题
- 3、怎么用几何的方法证明空间的平面共面?
- 4、高中立体几何:平面和面有什么区别?
- 5、平面与平面的关系?空间几何
- 6、平面与几何体的一个面重合叫什么
观察图中的两个几何体,它们分别有几个面?是平面还是曲面?面与面相交的...
第一个图形4个面围成,面与面相交4条直线两条曲线。第二个7个面围成,直线有14条,没有曲线。
有4个面;一个长方形,两个半圆,一个曲面。面与面相交成6条线。4条直线,2条曲线。

四个面,不都是平的,四个面相交成6条线,不都是直的,有4条是直的,两条是曲线。
关于画法几何里平面与平面的交线画法问题
1、事实上,总是先画出两个相交的平面,从而先有了两条交线。或者另外的做法是:先画出一个长方体,从中找到自己需要的两个面以及交线。
2、要画几何体中平面α与平面β的交线,可以先在平面α中画任意两条与平面β均不平行的直线,分别与平面β交于A,B两点(A,B不能重合),连接AB,那就是平面α与平面β的交线。
3、现在已经有一个公共点a,再找到一个公共点即可得到两平面交线。在投影图中连接eb,交ad为f,过XO做ff垂直XO。
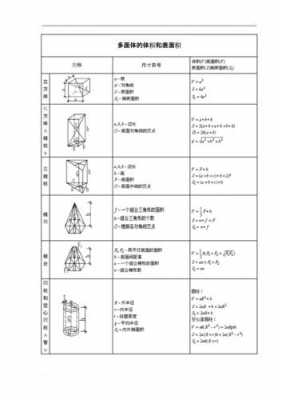
4、方法1,过B点作A1C1的平行线即是直线L.方法2,过A1点作C1B的平行线交DA延长线于E,过C1点作A1B的平行线交DC延长线于F,过EF两点的直线就是直线L,L必定经过B点。
5、个两个平面的公共点。如图,四棱锥P-ABCD中,ABCD是菱形,做出平面PAD与平面PBC的交线;P为1个公共点,需再找1个公共点即可,延长AD,BC交于E,那么E是第2个公共点,连接PE,则PE为两个平面的交线。
怎么用几何的方法证明空间的平面共面?
1、以下是证明共面的方法:给定空间直角坐标系,如果四个点的坐标满足以下等式:x1=x2+x3+x4,y1=y2+y3+y4,z1=z2+z3+z4。证明:假设点 A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3),D(x4,y4,z4)。
2、在第一种方法:任取这4点中2点做一条直线,证明做出的2条直线相交、平行、或重合即可。第二种方法:任取4点中3点做一个平面,再证明此平面经过这个点。第三种方法:若其中有3点共线,则此4点一定共面。
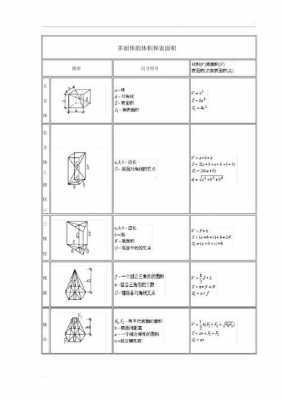
3、第一种方法:任取这4点中2点做一条直线,证明做出的2条直线相交、平行、或重合即可。第二种方法:任取4点中3点做一个平面,再证明此平面经过这个点。第三种方法:若其中有3点共线,则此4点一定共面。
4、在空间向量中,可以利用四点共面来求出四个点的外法向量的值。在平面几何中,可以利用四点共面来证明一些定理和性质。例如,可以利用四点共面来证明三角形三边中垂线交于一点。
高中立体几何:平面和面有什么区别?
平面图形和立体图形区别:平面图形中的所有点都在同一个平面内,而立体图形中的点不全在同一个平面内。
面条的面是指面粉,面粉做出来的才叫面条;平面的面是一个几何意义上的概念。
性质不同 平面图:可以把测区内的地面景观可沿垂直方向投影到平面上,并可按规定的符号和比例缩小相似的图形。立面图:房屋在与房屋立面平行的投影平面上所作的正投影,称为建筑物的立面。
概念不一样。平面图形是存在于一个平面上的图形,立体图形是由一个或者多个平面形成的可以存在于现实生活的。形体特点不一样。平面图形是只有一个面,而立体图形有多个面组成,有上面、左面、侧面、下面等。
平面与平面的关系?空间几何
平面与平面相交:两平面相交是两平面间的一种位置关系。如果两个平面只有一条公共直线,就说这两个平面有相交位置关系,简称两平面相交。这两个平面称为相交平面,而这条公共直线称为这两个平面的交线。
空间两个平面的位置关系有两种:相交和平行。垂直是相交的特殊情况。平行定义:如果两个平面没有公共点,则称这两个平面互相平行。平行判定: 如果一个平面内有两条相交直线都平行另一个平面,那么这两个平面平行。
两个平面之间的关系可以借助平面的法向量来判断。两个平面的法向量分别为 (1/2,1/3,1/4)和(2,3,-4)。显然这两个向量既不平行也不垂直,所以两个平面既不平行也不垂直,选A。
理论上存在两种可能,两平面既不平行也不相交。第一种 两个平面分别在两个不同的空间,且两个空间不相连。第二种,空间无意义。也就是空间不存在的情况,此时平面与平面无空间关系。
*平面图形组成空间几何体的角度不变。3*空间几何体每一个面的角的大小与平面图形的角相等。4*制作过程说明平面图形可以折成立体图形。立体图形可以展开为平面图形。
平面与几何体的一个面重合叫什么
轴线(axis),一般是指把平面或立体分成对称部分的直线;是指一个物体或一个三维图形绕着旋转或者可以设想着旋转的一根直线。轴线,又可以称为“中轴线”、“中心线”。
在数学中,两个平面图形如果形状和大小完全相同,则称它们为全等图形。全等图形可以通过平移、旋转和镜像来重合,而不需要改变其形状和大小。立体图形是三维的,它们由面、边和顶点组成。
就获得几何体的概念,在几何学中,人们把若干几何面(平面或曲面)所围成的有限形体称为几何体。围成几何体的面称为几何体的界面或表面,不同界面的交线称为几何体的棱线,不同棱线的交点称为几何体的顶点。
到此,以上就是小编对于平面几何计算公式的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏