本篇目录:
随机过程,2.8题求解答!
数学上的随机过程可以简单的定义为一组随机变量,即指定一参数集,对于其中每一参数点t指定一个随机变量x(t)。
{W(t), t≥0}, σt, 是一个维纳过程. X(t)=W(t)-aW(t-h), t≥0, h0 是常数. 求:X(t)的一维概率密度分布函数。

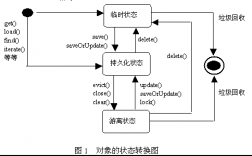
先要验证状态空间是否为本质类,即就是整个状态空间是一个闭集,且为最小闭集,本题是一个极端例子,用它可以说明无限多个非本质类的并集是闭集。
一道随机过程的题目,高分悬赏,有点实力的进!!!
(下位应用题,要过程)关于xy的方程组,{3x-y=5 4ax+5by=-22 与{2x+3y=-4 ax-by=8有相同解,求a、b的值。
解:(1)由压强公式:P=ρgh,其中ρ为液体密度。
当两个三角形的高相等时,面积的比就等于底的比。连接DC。SADE:SADC=1:(1+2)=1:3 ,SADC:SABC=2:(2+1)=2:3 ,所以 SADE:SABC=(SADE:SADC)×(SADC:SABC)=1/3*2/3=2/9=2:9 。

这个题目标准做法我认为是 找到这个平面区域:为三角形,且顶点已知为(0,0)、(0,2)、(4,0)要求原面积最小 即是在求半径最小的圆。
随机过程解答?
1、随机过程(A)解答(15分)设随机过程,是相互独立服从正态分布的随机变量。1)求的一维概率密度函数;2)求的均值函数、相关函数和协方差函数。
2、{W(t), t≥0}, σt, 是一个维纳过程. X(t)=W(t)-aW(t-h), t≥0, h0 是常数. 求:X(t)的一维概率密度分布函数。
3、设随机过程X 变量。试求X 解:(t )=X cos ω0t ,-∞ (t )的一维概率分布。

4、随机过程及其在金融领域中的应用习题五答案如下:确定概率模型:首先需要明确问题是关于什么事件的概率,这个事件是由哪些基本事件构成的,以及每个基本事件的发生概率是多少。
5、随机过程就是许多随机变量的集合,代表了某个随机系统随着某个指示向量的变化,这个指示向量常用的是 时间向量。其中 指标集合T : 通常用的指标集合是代表时间,以实数或整数表示其元素。
随机过程第二章期末练习题
1、应用统计与随机过程课程习题集湖南大学信息科学与工程学院第二章练习题判断题确定信号为特殊的随机信号,如果称某个确定信号为平稳的,意味着该信号为常量。
2、练习1设,试求Y的概率密度函数.练习2设随机变量X在(0,1)区间内服从均匀分布,试求(1)的概率密度函数(2)的概率密度函数随机过程巩固练习1设随机过程为常数,V为服从正态分布N(0,1)的随机变量。
3、随机过程期末复习题库(2015)填空题对于具有常数均值的二阶矩过程数只与,为宽平稳过程当且仅当二元函有关,而与和无关。
随机过程练习(第二章)
第二章随机过程分析1学习指导1要点随机过程分析的要点主要包括随机过程的概念、分布函数、概率密度函数、数字特征、通信系统中常见的几种重要随机过程的统计特性。
应用统计与随机过程课程习题集湖南大学信息科学与工程学院第二章练习题判断题确定信号为特殊的随机信号,如果称某个确定信号为平稳的,意味着该信号为常量。
则将g(x)在其定义与上分成若干个单调分支,在每个单调分支上应用(1)的结果得Y=g(X)的概率密度函数为其中I是在每个单调分支上按照(1)确定的y的取值公共部分。
到此,以上就是小编对于随机过程课程设计的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏