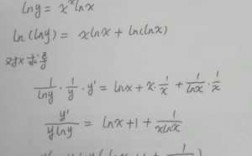本篇目录:
- 1、完全平方公式的推导过程
- 2、用完全平方公式解题,要计算过程
- 3、完全平方公式的推导过程是怎样的?
- 4、如何证明完全平方公式和平方差公式?
- 5、...方形请用图中空白长方形的面积来验证完全平方公式
- 6、如何用拼图的方法验证平方差公式及完全平方公式
完全平方公式的推导过程
1、完全平方公式推导过程:(a+b)=(a+b)(a+b)=a*a+b*a+a*b+b*b (展开,各项相乘)=a+2ab+b (合并同专类属项)。
2、完全平方公式的推导过程可以通过多项式的乘法得出。假设有一个二次三项式ax的平方加上bx加上c,我们可以将其写成(ax+b)乘以(x+c)的形式,然后展开得到ax的平方加上(bc+ac)x加上bc的平方。

3、解答过程如下:(a+b)。=(a+b)(a+b)。=a+ab+ab+b。=a+2ab+b。以上内容解释:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
用完全平方公式解题,要计算过程
完全平方公式是指 $(a+b)^2 = a^2 + 2ab + b^2$ 这个公式。如果你需要计算 $(a+b)^2$,可以使用下面的简便计算方法:将 $a$ 的平方 $a^2$ 和 $b$ 的平方 $b^2$ 分别计算出来。
完全平方公式计算题如下:(x+1)-4x。(2x-y)-2(2x-y)+1。(x+y)-2(x-y)+(x-y) 。(a+1)(a+5)+4。
x-y= xy= (x+y)^2=(x-y)^2+4xy=16+20=36,x+y=-6或 6注意到xy,x,y同号,且x-y=4所以x,y0.因此x+y=6 x^2+y^2=(x-y)^2+2xy=16+10=26 x+y=7。

平方差公式是先平方再减 a-b= (a+b)(a-b)。完全平方公式是先加减最后是平方 (a±b)=a±2ab+b。
完全平方公式的推导过程是怎样的?
1、完全平方公式推导过程:(a+b)=(a+b)(a+b)=a*a+b*a+a*b+b*b(展开,各项相乘)=a+2ab+b(合并同专类属项)。
2、完全平方公式推导过程如下:(a+b)=(a+b)(a+b)=a*a+b*a+a*b+b*b(展开,各项相乘)=a+2ab+b(合并同专类属项)。
3、完全平方公式的推导过程可以通过多项式的乘法得出。假设有一个二次三项式ax的平方加上bx加上c,我们可以将其写成(ax+b)乘以(x+c)的形式,然后展开得到ax的平方加上(bc+ac)x加上bc的平方。

4、完全平方公式是进行代数运算与变形的重要的知识基础。
如何证明完全平方公式和平方差公式?
1、完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。平方差公式:一个平方数或正方形,减去另一个平方数或正方形得来的乘法公式。
2、平方差公式是指两个数的平方差可以用以下公式表示:a-b=(a+b)(a-b).这个公式可以在异或运算中得到应用。
3、(a-b)2=a2+b2-2ab 两数差的完全平方公式(完全平方差)都叫做完全平方公式。
4、平方差公式:a^2-b^2=(a+b)*(a-b)。完全平方公式:a^2±2a*b+b^2=(a±b)^2。
5、完全平方公式数学表达式为:完全平方和公式(a+b)=a+2ab+b和完全平方差公式(a-b)=a-2ab+b。即两个数和或差的平方等于它们的平方和加上或减去它们积的两倍。
6、完全平方差公式:(a-b)2=a2-2ab+b2,完全平方差:两数差的平方,等于它们的平方和,减去它们的积的2倍即完全平方公式。
...方形请用图中空白长方形的面积来验证完全平方公式
(a+b)=a+2ab+b、(a-b)=a-2ab+b。完全平方公式是一个数学名词,一个常用的简便计算公式。
长方形的面积公式:长方形的面积=长x宽,用字母来表示s=ab,其中,a表示长方形的长,b表示长方形的宽。这是人教版三年级下册第五单元的学习内容。长方形长的那条边叫长,短的那条边叫宽。
长方形:面积=长×宽(S=ab)正方形:面积=边长×边长(S=a)长方体和正方体有体积公式:长方体:长方体的体积=长×宽×高。
如图,大的长方形面积等于四个小长方形面积之和:(x + p) * (x + q) = x*x + p*x + q*x + p*q。当 p = q = y 时,就是完全平方公式:(x + y)^2 = x^2 + 2xy + y^2。
如何用拼图的方法验证平方差公式及完全平方公式
1、用几何图形说明完全平方公式:(1)(a+b)=a+2ab+b。(2)(a-b)=a-ab-ab+b=a-2ab+b。
2、完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。平方差公式:一个平方数或正方形,减去另一个平方数或正方形得来的乘法公式。
3、完全平方公式 完全平方公式是指一个整数的平方可以表示成两个连续自然数之和或两个连续自然数之差的平方。例如,我们可以将整数n的平方表示为(n-1)+(n-1)+n或(n+1)-(n+1)-n。
到此,以上就是小编对于完全平方公式验证过程视频的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏