本篇目录:
- 1、如何理解随机变量和随机过程?
- 2、什么是随机过程?什么是平稳随机过程,非平稳随机过程
- 3、请根据实际举例说明何谓随机过程?在何种条件下成为平稳过程?
- 4、随机过程的定义
- 5、随机过程解答?
- 6、随机过程中的平稳和各态历经
如何理解随机变量和随机过程?
随机变量(random variable):简单的随机现象,如某班一天学生出勤人数,是静态的。 随机过程(stochastic process):随机现象的动态变化过程。动态的。如某一时期各个时刻的状态。
一个实际的随机过程是任意一个受概率支配的过程,例子有:①看做是受孟德尔遗传学支配的群体的发展;②受分子碰撞影响的微观质点的布朗运动,或者是宏观空间的星体运动;③赌场中一系列的赌博;④公路一指定点汽车的通行。

随机过程就是许多随机变量的集合,代表了某个随机系统随着某个指示向量的变化,这个指示向量常用的是 时间向量。其中 指标集合T : 通常用的指标集合是代表时间,以实数或整数表示其元素。
什么是随机过程?什么是平稳随机过程,非平稳随机过程
1、即若一个随机过程的数学期望及方差与时间无关,而其相关函数仅与有关,即我们就称这个随机过程是广义平稳的。
2、随机过程(Stochastic Process)是一连串随机事件动态关系的定量描述。在这里我们主要研究平稳随机过程。平稳随机过程:狭义平稳概念:所谓平稳随机过程,是指它的任何n维分布函数或概率密度函数与时间起点无关。
3、平稳信号和非平稳信号都是随机信号,区别在于特性和定义不同。随机信号是随机过程,其每个时间点都是一个随机变量。
4、在数学中,平稳随机过程或者严平稳随机过程又称狭义平稳过程。
5、随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。
请根据实际举例说明何谓随机过程?在何种条件下成为平稳过程?
1、process),又称狭义平稳过程,是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程:即随机过程的统计特性不随时间的推移而变化。这样,数学期望和方差这些参数也不随时间和位置变化。
2、在数学中,平稳随机过程或者严平稳随机过程又称狭义平稳过程。

3、随机变量可以是连续的也可以是离散的。若一个随机过程的均值和方差不随时间的改变而改变,且在任何两期之间的协方差值仅依赖于两期的距离或滞后的长度,而不依赖于时间,这样的随机过程称为平稳性随机过程。
4、X(t2),···,X(tn))和(X(t1+h),X(t2+h),···,X(tn+h))具有相同的分布函数,则称随机过程{X(t),t∈T}具有平稳性,称此过程为严平稳随机过程,简称随机过程。
5、一个随机过程平稳表明该过程进入一种 稳态。严平稳是一种条件比较苛刻的平稳性定义,它认为只有当序列 所有的统计性质 都不随着时间的推移而发生变化时,该序列才能被认为平稳。
随机过程的定义
1、按有无平稳性分为:平稳随机过程和非平稳随机过程; 按有无各态历经分为:各态历经随机过程和非各态历经随机过程; 按功率谱特性分为:白色过程和有色过程,宽带过程和窄带过程。
2、通俗地说,随机过程是所有可能实现的所构成的总体。
3、随机变量是指在同一条件下,事件每次发生的结果是随机的、不确定的,而随机过程是指在同样条件下,事物发生的某一过程是随机的、不可准确预知的。
4、从信号分析的角度来说,随机信号和噪声都是随机过程。随机过程是一笼统的概念,平常指的是随机过程的任一实现。
5、基本定义 随机过程就是一族随机变量{ X(t), t},其中,t是参数,它属于某个指标集T,T称为参数集。注:注意区分随机变量与随机过程。
6、一般来说,把一组随机变量定义为随机过程。在研究随机过程时人们透过表面的偶然性描述出必然的内在规律并以概率的形式来描述这些规律,从偶然中悟出必然正是这一学科的魅力所在。
随机过程解答?
=(1+sin t 1sin t 2+cos t 1cos t 2) 31=1+cos (t 1-t 2). 3 设随机过程X (t 0),其中X 是具有分布密度f (x )的随机变量。
随机过程(A)解答(15分)设随机过程,是相互独立服从正态分布的随机变量。1)求的一维概率密度函数;2)求的均值函数、相关函数和协方差函数。
维纳过程是独立增量过程。知道了这一点,以下是计算问题。--- {W(t), t≥0}, σt, 是一个维纳过程. X(t)=W(t)-aW(t-h), t≥0, h0 是常数. 求:X(t)的一维概率密度分布函数。
均值是cost+sint , 方差是4, 自相关函数是5cos(t1-t2)+sin(t1-t2), 该过程是两个正态过程之和,故亦为正态过程,参考之前的均值和方差,可给出一维概率密度。
随机过程中的平稳和各态历经
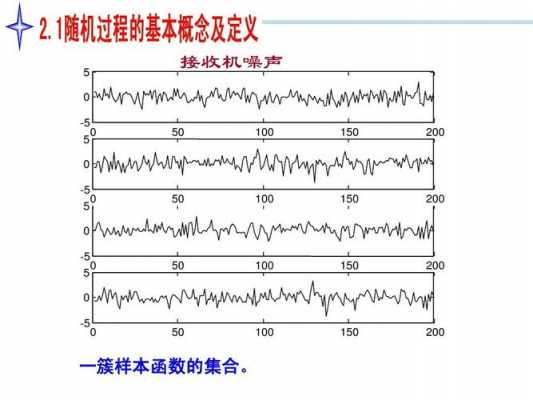
1、所谓各态历经,是指可以从过程的一个样本函数中获得它的各种统计特性;具有这一特性的随机过程称为具有各态历经性的随机过程,只要有一个样本函数就可以表示出它的数字特征。
2、对于具有这种性质的历经性随机过程,称它具有各态历经性,或遍历性。平稳随机过程的各态历经性可以理解为,随机过程的各个样本都同样经历随机过程的各种可能状态联系。
3、广义平稳概念:若一个随机过程的数学期望及方差与时间无关,而其相关函数仅与τ有关,则称这个随机过程为广义平稳随机过程。
4、平稳随机过程的均值与时间无关,是一个常数。平稳随机过程的自相关函数只与计算时取的时间间隔有关。满足以上两点,就是广义平稳随机过程,也可以理解为各态历经性。
5、平稳二项随机过程定义:平稳随机过程的均值与时间无关,是一个常数,平稳随机过程的自相关函数只与计算时取的时间间隔有关。满足以上两点,就是广义平稳随机过程,也可以理解为各态历经性。
6、平稳随机过程的重要特性:平隐随机过程在满足一定条件下有一个非常重要的特性,称为各态历经性。
到此,以上就是小编对于循环平稳信号处理与应用的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏