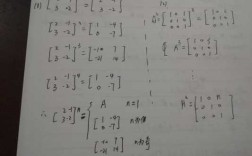本篇目录:
- 1、求矩阵方程的解。有详细过程
- 2、如何求矩阵的特征方程?
- 3、求解矩阵方程如图
求矩阵方程的解。有详细过程
解答过程如下:可以用这两种方法解初等变换法:有固定方法,设方程的系数矩阵为A,未知数矩阵为X,常数矩阵为B,即AX=B,要求X,则等式两端同时左乘A^(-1),有X=A^(-1)B。
矩阵方程的解法可以通过代入法、加减消元法、逆矩阵法等方法进行求解。具体步骤如下:假设矩阵方程为Ax=b,其中A为给定的矩阵,b为给定的向量。代入法:将方程中的未知数b代入已知条件中,找到一组解。

初等变换法:有固定方法,设方程的系数矩阵为A,未知数矩阵为X,常数矩阵为B,即AX=B,要求X,则等式两端同时左乘A^(-1),有X=A^(-1)B。
如何求矩阵的特征方程?
1、特征方程等于:|λE-A|={[(λ+2),0,4],[-1,λ-1,-1],[-1,0,λ-3]}=0。
2、齐次线性方程组 (a-e)x=0 有 2 个线性无关的解,即有 2 个基础解系。基础解系的个数 2,等于未知数的个数 3,减去系数矩阵 a-e 的秩,则 系数矩阵 a-e 的秩 为 1。
3、用行列式变化,化为三角矩阵就可以了:以上,请采纳。
4、你上面那个是求特征值用的行列式吧,行列式展开后得下面那个 所以特征值是1,2,5 行列式的计算建议你看一下书,有很多种计算方法的。当然3阶以下的行列式可以直接展开,你也可以初等变换之后再展开。
求解矩阵方程如图
1、将矩阵方程化为 (A-E)X=A 方法1:求出(A-E)的逆,再两边左乘以(A-E)的逆。方法2:拼成矩阵(A-E,A)运用行初等变换,当把A-E化为单位矩阵时,A就化为了要求的矩阵X。
2、当A可逆时,矩阵方程XA=B有唯一解X=BA^(-1),可以通过初等列变换较为简便地求解,原理如图。以下采用初等列变换求矩阵方程的解,过程如图。当然也可以先求出A的逆矩阵,再与矩阵B作乘法,不过会相对复杂一些。
3、代数余子式Aij=(-1)∧(i+j)Mij。余子式Mij等于去掉i行和j列后的所有元素组成的行列式的值。
4、如图所示供参考。化简,用分块矩阵法,解线性非齐次方程组,即得答案。
5、AX=B X=A^(-1)B A^(-1)=A*/|A| |A|=-1 因此讲问题转化为了求A的伴随矩阵A 这里不好写,如图所示。
6、线性代数增广矩阵。初等行变换,增广矩阵,可逆矩阵,矩阵乘法。如图所示请采纳谢谢。
到此,以上就是小编对于薪酬结构划分矩阵的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏