自回归模型过程（自回归模型定义）-义乌市趣迅电子商务商行

本篇目录：

1、其表达形式为y = wx+e，e为误差服从均值为0的正态分布。线性回归模型是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。

2、因变量是我们关心的变量，通常表示某种结果或效应。自变量是可能影响因变量的变量，可以是有意识的操纵的变量（实验中的独立变量）或者是观察到的变量（系统中的其他变量）。回归分析的目标是理解自变量如何影响因变量。

3、自变量（Independent variable）一词来自数学。在数学中，y=f（x），在这一方程中自变量是x，因变量是y。

4、确定变量：明确定义了预测的具体目标，并确定了因变量。如果预测目标是下一年的销售量，则销售量Y是因变量。通过市场调查和数据访问，找出与预测目标相关的相关影响因素，即自变量，并选择主要影响因素。

5、服从正态分布N(0，σ2) 。其方差σ2 = var (ei) 反映了回归模型的精度， σ 越小，用所得到回归模型预测y的精确度愈高。e 的大小不随所有变量取值水平的改变而改变，即方差齐性。

6、表示。其中x叫做自变量，y叫做因变量。经典在某个坐标变化过程中，如果有两个变量x和y，对每一个给定的x值，y都有唯一确定的值与它对应，确定y=x的函数。x=自变量，y作为x的因变量。

自回归滑动平均模型（ARMA 模型，Auto-Regressive and Moving Average Model）是研究时间序列的重要方法，由自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。

全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model，简记ARIMA)，是由博克思(Box)和詹金斯(Jenkins)于70年代初提出一著名时间序列预测方法1，所以又称为box-jenkins模型、博克思-詹金斯法。

ARIMA（p，d，q）中，AR是自回归，p为自回归项数；MA为滑动平均，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

显然，ARMA模型描述的是一个时不变的线性系统。？具有AR阶数p和MA阶数Q的ARMA过程常记作用ARMA（p，q）。

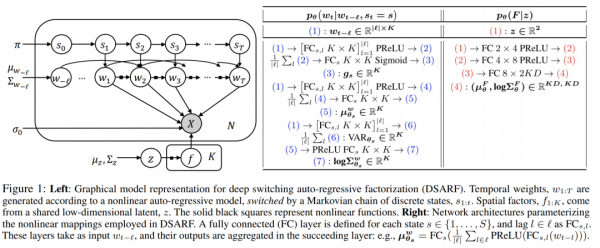
ARMA模型(auto regressive moving average model)自回归滑动平均模型，模型参量法高分辨率谱分析方法之一。这种方法是研究平稳随机过程有理谱的典型方法，适用于很大一类实际问题。

1、ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），时间序列预测分析方法之一。

2、所谓ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

3、ARIMA模型的全称叫做自回归移动平均模型，全称是(ARIMA， Autoregressive Integrated Moving Average Model)。也记作ARIMA(p，d，q)，是统计模型(statistic model)中最常见的一种用来进行时间序列预测的模型。

4、ARIMA模型是针对非平稳时间序列建模。换句话说，非平稳时间序列要建立ARMA模型，首先需要经过差分转化为平稳时间序列，然后建立ARMA模型。ARIMA模型的原理。正如前面介绍，ARIMA模型实际上是AR模型和MA模型的组合。

5、正如前面介绍，ARIMA模型实际上是AR模型和MA模型的组合。 AR模型的形式如下：其中：参数为常数，是阶自回归模型的系数；为自回归模型滞后阶数；是均值为0，方差为的白噪声序列。模型记做——表示阶自回归模型。

6、ARIMA模型全称为差分自回归移动平均模型(AutoregressiveIntegratedMovingAverageModel，简记ARIMA)，是由博克思(Box)和詹金斯(Jenkins)于70年代初提出的一著名时间序列预测方法，所以又称为box-jenkins模型、博克思-詹金斯法。

到此，以上就是小编对于自回归模型定义的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。