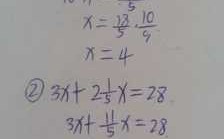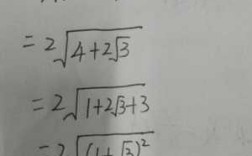求和求和公式推导过程（求和公式法则）-义乌市趣迅电子商务商行

本篇目录：

等差数列基本公式：末项=首项+(项数-1)*公差项数=(末项-首项)÷公差+1首项=末项-(项数-1)*公差和=(首项+末项)*项数÷2末项：最后一位数首项：第一位数项数：一共有几位数和：求一共数的总和。

等差数列求和公式如下：Sn = n(a1 + an)/2，其中，Sn表示数列前n项的和，a1表示数列的第一项，an表示数列的第n项，n表示数列中的项数。

项数的计算方法是末项减去首项除以项差（每项之间的差）加1。进一步归纳得到等差数列求和公式：Sn＝（a1＋an）n／2　Sn＝n（2a1＋（n－1）d）／2； d＝公差　Sn＝An2＋Bn； A＝d／2，B＝a1－（d／2）。

等差数列求和公式推导：sn=a1+a2+a3+an。把上式倒过来得：sn=an+an-1+a2+a1。将以上两式相加得：2sn=（a1+an）+（a2+an-1）+（an+a1）。由等差数列性质：若m+n=p+q则am+an=ap+aq得2sn=n（a1+an）。

等差数列求和公式及推导如下：等差数列前n项和公式为是Sn=a1*n+[n*(n-1)*d]/2或Sn=[n*(a1+an)]/2。

1、求和公式如下：(1)等比数列：a(n+1)/an=q(n∈N)。

2、求和公式是S=(1+n)*n/2，求S实质上是求{an}的通项公式，应注意对其含义的理解。常见的方法有公式法、错位相减法、倒序相加法、分组法、裂项法、数学归纳法、通项化归、并项求和。

3、前n项和公式为：Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2 (n属于自然数）。a1为首项，an为末项，n为项数，d为等差数列的公差。

4、求和计算公式是一种数学公式，用于计算一系列数字的总和。求和计算公式的具体形式为：Σ（希腊字母sigma，代表总和的意思），后面跟着每一个需要求和的项用括号括起来，括号前面是该项的序号，从1开始，最后一个项的序号为n。

5、求总和的公式可以表示为Σ（an）。求总和的公式是指对一个数列或一组数据进行求和的公式。在数学中，求总和的公式通常使用符号“Σ”表示，它表示对一个数列中所有数的累加和。

6、求和公式：首项加末项的和乘以项数除以二是等差数列的求和公式，即若一个等差数列的首项为a1，末项为an，那么该等差数列和表达式为：S=n（a1+an）÷2，就是（首项+末项）×项数÷2。

连续自然数求和公式是指1到n的自然数之和可以用公式n（n+1）/2来计算。这个公式的推导过程可以通过以下步骤来解释：我们可以观察1到n的自然数之和如何计算。

a(n)=a1+(n-1)d。Sn=na1+n*(n-1)d/2。等差数列前N项和公式S=(A1+An)N/2。等差数列公式求和公式 Sn=n(a1+an)/2或Sn=na1+n(n-1)d/2。

就得到一个常数列的和，这一求和方法称为倒序相加法。我们在学知识时，不但要知其果，更要索其因，知识的得出过程是知识的源头，也是研究同一类知识的工具，例如：等差数列前n项和公式的推导，用的就是“倒序相加法”。

n方的求和公式是：San=a1(1-a^n)/(1-a)=a(a^n-1)/(a-1)。

n是大于1的整数）等于a，那么这个数叫做a的n次方根。当n为奇数时，这个数为a的奇次方根；当n为偶数时，这个数为a的偶次方根。求一个数a的n次方根的运算叫做开n次方，a叫做被开方数，n叫做根指数。

到此，以上就是小编对于求和公式法则的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。