本篇目录:
- 1、如何理解卷积逆系统的概念?
- 2、卷积的逆运算怎么求?
- 3、请问u(t)*u(t-1)卷积怎么算???
- 4、上池化(unpooling),上采样(unsampling)和反卷积(deconvolution)的区别...
如何理解卷积逆系统的概念?
1、所以画出方程式左端两个冲激函数的图形,就是在t t两个点有两个向上的无穷大的坐标。
2、从“积”的过程可以看到,我们得到的叠加值,是个全局的概念。以信号分析为例,卷积的结果是不仅跟当前时刻输入信号的响应值有关,也跟过去所有时刻输入信号的响应都有关系,考虑了对过去的所有输入的效果的累积。
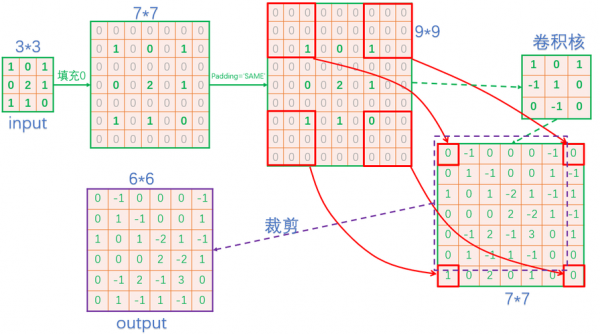
3、卷积的通俗理解就是所谓两个函数的卷积,本质上就是先将一个函数翻转,然后进行滑动叠加。应用场景: 信号分析。
4、如果还是对卷积的含义不太明白,下面是 对卷积的另外解释 :卷积表示为y(n)=x(n)h(n) ,x(n)表示的是系统的输入,y(n)表示的是系统的输出,h(n)表示的是相应函数。
5、卷积的概念还可以推广到数列、测度以及广义函数上去。应用领域 在数字图像处理中,卷积滤波在边缘检测和相关过程的许多重要算法中起着重要作用。 在光学领域,离焦照片是清晰图像与镜头功能的卷积。
6、设 IF表示傅立叶逆变换,则 因此有 故频域卷积定理得证。
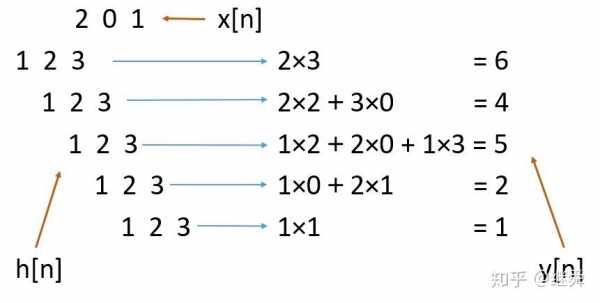
卷积的逆运算怎么求?
积分运算公式:∫0dx=C(2)=ln|x|+C。积分是微分的逆运算,即知道了函数的导函数,反求原函数。
逆卷积:证明卷积运算具有逆运算。这意味着对于任意函数h(t),我们可以找到一个函数f(t),使得h(t)=f(t)*g(t)。这个函数f(t)被称为h(t)的逆卷积或解卷积。
底=2面积/高,高=2面积/底。三角形的逆运算公式是已知三角形的面积和其他两边其中一边的长度,求另一边的长度。例如已知三角形的面积和底,求高公式为:高=2面积/底,求低公式为:低=2面积/高。
第一 载波和信号不是通过卷积,而是调制。第二 我不清楚什么叫做卷积的逆运算,请搞清楚概念。第三 卷积的意思指的是信号在频域上相乘,一般是过滤波器时需要,而不是再调制的时候。
即为导函数的逆运算, 从求值变成求函数. 对于不定积分求解,我们需要使用积分表或积分公式来求解.积分公式是用来解决不定积分问题的常用工具。
请问u(t)*u(t-1)卷积怎么算???
1、tut卷积ut这么算的:u(t)*u(t-1)=u(t)*u(t)*δ(t-1)=tu(t)*δ(t-1)=(t-1)u(t-1)。卷积是分析数学中一种重要的运算。
2、利用积分性质,一个积分一个求导,然后在卷积。
3、卷积的计算公式和步骤如下:计算公式 f(t)*g(t)=∫f(τ)g(t-τ)dτ。步骤 对函数f(t)和g(t)进行离散化处理,变为离散信号。
上池化(unpooling),上采样(unsampling)和反卷积(deconvolution)的区别...
反卷积在CNN中常用于表示一种反向卷积 ,但它并不是一个符合严格数学定义的反卷积操作。与上池化不同,使用反卷积来对图像进行上采样是可以习得的。通常用来对卷积层的结果进行上采样,使其回到原始图片的分辨率。
upsampling(上采样)的三种方式: Resize ,如双线性插值直接缩放,类似于图像缩放; 反卷积 (deconvolution & transposed convolution); 反池化 (unpooling)。
unpooling的操作与unsampling类似,区别是unpooling记录了原来pooling是取样的位置,在unpooling的时候将输入feature map中的值填充到原来记录的位置上,而其他位置则以0来进行填充。
到此,以上就是小编对于卷机定理的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏