本篇目录:
- 1、我想成为数学奇才,想问问一步一步的要学什么看什么书,自学!因为我超级...
- 2、判断随机过程的独立中的问题
- 3、求大学本科从大一到大四的数学教材与出版社名称.
- 4、初识数学大师柯尔莫哥洛夫(Kolmogorov)
- 5、可以推荐一些好的随机过程书籍吗
我想成为数学奇才,想问问一步一步的要学什么看什么书,自学!因为我超级...
1、如果是想自学初中祷告中的数学,那么你可以买重难点手册,因为上面的讲解很详细,也很清楚,并且有课本上的答案。重难点突出。需要掌握的题型也长讲的比较好。
2、链接:https://pan.baidu.com/s/1znmI8mJTas01m1m03zCRfQ ?pwd=1234 提取码:1234 简介:高中数学优质资料下载,包括:试题试卷、课件、教材、视频、各大名师网校合集。

3、然后找小学数学总复习的资料写一写,书店里的都不错,找本你喜欢的就行了。接着可以用这个方法继续学初中、高中的数学。(看课本、做笔记、做课本练习、做总复习资料)。
4、初中数学合集百度网盘下载 链接:https://pan.baidu.com/s/1znmI8mJTas01m1m03zCRfQ ?pwd=1234 提取码:1234 简介:初中数学优质资料下载,包括:试题试卷、课件、教材、视频、各大名师网校合集。
5、高中数学课的设置 高中数学内容丰富,知识面广泛,将有:《代数》上、下册、《立体几何》和《平面解析几何》四本课本,高一年级学习完《代数》上册和《立体几何》两本书。高二将学习完《代数》下册和《平面解析几何》两本书。
判断随机过程的独立中的问题
1、一个随机过程是二阶矩过程,则它的4个数字特征均存在。一个随机过程的数字特征是:均值函数、方差函数、协方差函数和自相关函数。从测度论的角度讲,随机变量的均值是不一定存在的。

2、解题思路:本题先求出联合分布,在判断独立性时,若联合分布有零元,但边缘分布不全为零,则随机变量不独立。
3、不相关就是两者没有线性关系,但是不排除其它关系存在,独立就是互不相干没有关联。对于均值为零的高斯随机变量,“独立”和“不相关”等价的。
4、分别算出x、y的边缘概率密度。f(x) = ∫(-x,x)f(x,y)dy = 2x f(y) = ∫(y,1)f(x,y)dx = 1-y, y0 ∫(-y,1)f(x,y)dx = 1+y,y0 显然,f(x,y)≠f(x)*f(y)所以不独立。
5、E(aX+bY)=aE(X)+bE(Y);D(aX+bY)=a^2D(X)+2abCov(X,Y)+b^2D(Y);其中Cov(X,Y)表示X,Y的协方差。这是概率论中的经典公式,任何有关概率的书上都有。

6、黄,兰颜色的事件.得 P(A)=P(B)=P(C)=2/4=1/2,P(AB)=P(AC)=P(BC)=1/4 则可得A,B,C两两独立!但P(ABC)=1/4,并不等于P(A)P(B)P(C)=1/故此时A,B,C不相互独立。
求大学本科从大一到大四的数学教材与出版社名称.
1、《高等数学》(同济大学出版社):这是一本经典的高等数学教材,内容全面且系统,涵盖了微积分、解析几何、线性代数等多个方面。
2、大一高等数学,每个大学,每个专业用的都有可能不同,但是通用的一般是同济大学出的上下2册的高等数学,还有的用的是北京大学出的3册的高等数学。我很喜欢北京大学出的3册的高等数学,是文丽,吴良大等编写的。
3、初等微积分学 示例教材:《高等数学(第六版)》同济大学应用数学教研室编,高等教育出版社。 线形代数 示例教材:《线性代数(物理类)》徐军民等编,兰州大学出版社。
4、自己认为计较牛的大学都有自己用的教材。但公认比较好的还是同济大学主编的,由高等教育出版社出版的《高等数学》,分上下册,现在已经出第六版了。
5、《数学的语言:化无形为可见》,很好地传授数学观念的书,作者是齐斯德福林。《高等数学》,是2009年同济大学出版社出版的图书,作者是同济大学数学系。
初识数学大师柯尔莫哥洛夫(Kolmogorov)
1、在莫斯科大学,柯尔莫哥洛夫听大数学家鲁津(N.N.Luzin,1883—1950)的课,且与鲁津的学生亚历山德罗夫(P.S.Alexandrov,1896—1982)、乌里松(P.S.Urysohn,1898—1924)、苏斯林(M.Y.Suslin)等有了学术上的频繁接触。
2、柯尔莫哥洛夫(1903~)Kolmogorov,Andrei Nikolaevich 苏联数学家。1903年4月25日生于中亚的顿巴夫。
3、安德列·柯尔莫哥洛夫(1903年4月25日-1987年10月20日),20世纪苏联最杰出的数学家,也是20世纪世界上为数极少的几个最有影响的数学家之一。他的研究几乎遍及数学的所有领域,做出许多开创性的贡献。
4、“lim[n→+∞]{(1/n)∑[1≤k≤n]ξk-(1/n)∑[1≤k≤n]Mξk}=0”的概率为【补充】:该定理由俄罗斯数学家A.N.柯尔莫哥洛夫提出。
可以推荐一些好的随机过程书籍吗
1、从另一方面来说,即使概率论方向的纯数学研究生也需要一本开拓视野,启发思维的简明扼要的随机过程教科书。
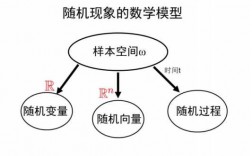
2、随机积分与伊藤引理 BSM微分方程与Feynman-Kac定理 概率论 随机过程 “随机过程”是从静态的概率论向动态的概率论过渡的基本概念。对于一个随机过程,取任意一个时点的状态,都是一个随机变量,这是随机过程的基本特征。
3、_1?ie=UTF8&qid=1308065476&sr=8-1 你要用的知识点书上都有,复杂的证明全都跳过了,例子不少。只是小错好多。。
4、《应用随机过程》一书主要对应用随机过程学的基础知识作了介绍,具体内容包括随机过程的基本概念和基本类型、Poisson过程、Markov链、Brown运动、随机积分等。
5、浙江大学和国防科技大学的《概率论与数理统计》这两本书写得都很好,两本书都网购了。我阅读以吴翊教授的书为主,浙大教材做参考书籍。
6、好的书籍推荐:《活着》、《百年孤独》、《红楼梦》、《小王子》、《围城》等。《活着》余华的《活着》是一部经典之作,讲述了主人公在社会变革下,与家人屡遭苦难的故事。
到此,以上就是小编对于随机过程 龚光鲁译pdf的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏