本篇目录：

• 1、如何求解椭圆的标准方程?
• 2、椭圆的标准方程公式
• 3、椭圆的方程如何求得?
• 4、椭圆的标准方程怎么求?

如何求解椭圆的标准方程?

当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。其中a^2-c^2=b^2。

在平面几何中，我们经常需要求解椭圆的标准方程。下面将详细介绍求解椭圆标准方程的方法，包括中心坐标、长轴半径、短轴半径和旋转角度等方面的求解过程。

当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)； 其中a^2-c^2=b^2。

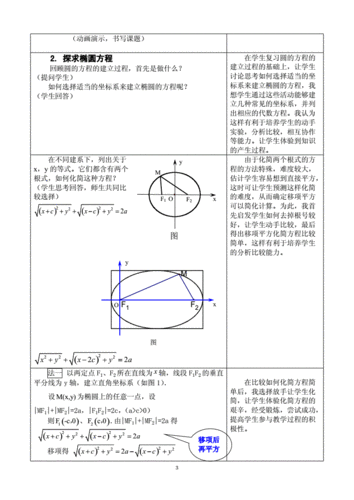
步骤1：确定椭圆的中心 椭圆方程的标准形式为：（x - h）^2 / a^2 + (y - k)^2 / b^2 = 1，其中（h，k）为椭圆的中心坐标。因此，在求解椭圆方程之前，首先需要确定中心坐标。

首先将分式中的常数移到等式右边，得到 x^2/16 = 1 - y^2/9。然后两边同乘以16，得到 x^2 = 16 - 16y^2/9。接着整理得到 x^2/16 + y^2/9 = 1，即椭圆的标准方程式。

椭圆的标准方程公式

椭圆的方程：椭圆可以用数学方程来描述。在笛卡尔坐标系中，椭圆的标准方程为(x/a)^2 + (y/b)^2 = 1，其中a和b分别是椭圆的半长轴和半短轴的长度。 椭圆的焦点性质：椭圆的一个重要性质是焦点定理。

椭圆的标准方程共分两种情况：当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)；当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。

椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)；当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)；其中a^2-c^2=b^2；推导：PF1+PF2F1F2(P为椭圆上的点 F为焦点)。

椭圆的标准方程 当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。其中a^2-c^2=b^2。

椭圆的一般式方程是：a+bx+cy+dxy+ex^2+fy^2=0，其中a、b、c、d、e、f，为任意椭圆方程的系数，该一般方程包含了标准椭圆的旋转和平移变换。

椭圆的标准方程共分两种情况：当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)；当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)；其中a^2-c^2=b^2。

椭圆的方程如何求得?

当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。其中a^2-c^2=b^2。

当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)； 其中a^2-c^2=b^2。

步骤1：确定椭圆的中心 椭圆方程的标准形式为：（x - h）^2 / a^2 + (y - k)^2 / b^2 = 1，其中（h，k）为椭圆的中心坐标。因此，在求解椭圆方程之前，首先需要确定中心坐标。

椭圆的极坐标方程形式是：r = a(1 - ε) / (1 - εcosθ)其中，r是点到原点的距离，θ是点与极轴的夹角，a是椭圆的半长轴长度，ε是离心率。椭圆是一个几何图形，具有两个焦点和一个长轴和短轴。

两边再平方，化简得 又 ，设 ，得 两边同除以 ，得 这个形式是椭圆的标准方程。通常认为圆是椭圆的一种特殊情况[2] 。非标准方程 其方程是二元二次方程，可以利用二元二次方程的性质进行计算，分析其特性[3] 。

椭圆的标准方程怎么求?

1、当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。其中a^2-c^2=b^2。

2、椭圆的方程：椭圆可以用数学方程来描述。在笛卡尔坐标系中，椭圆的标准方程为(x/a)^2 + (y/b)^2 = 1，其中a和b分别是椭圆的半长轴和半短轴的长度。 椭圆的焦点性质：椭圆的一个重要性质是焦点定理。

3、椭圆的标准方程共分两种情况：当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)；当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。

到此，以上就是小编对于椭圆方程计算技巧的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。