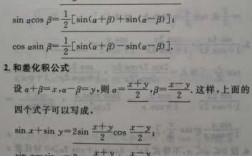本篇目录:
正弦、余弦、正切的公式分别怎么推导?
两角和(差)公式的正弦公式是:sin(α+β)=sinαcosβ+cosαsinβ。sin(α-β)=sinαcosβ-cosαsinβ。记忆方式:异名同号。正弦的展开肯定就是以正弦开头,然后满足异名,正弦配余弦,符号就和我们要求的符号相同。
正弦函数 sin(A)=a/c 余弦函数 cos(A)=b/c 正切函数 tan(A)=a/b 余切函数 cot(A)=b/a 其中a为对边,b为临边,c为斜边,通常的三角函数是在平面直角坐标系中定义的。

同理可推导余弦的万能公式。正切的万能公式可通过正弦比余弦得到。
正弦函数公式怎样推导的
1、是应用欧拉公式再求模。其详细过程,设z=x+iy。∵sinz=[e^(iz)-e^(-iz)]/(2i),将z=x+iy代.入。半径等于斜边并有长度 1,所以有了 sinθ=y/1。
2、两角和(差)公式的正弦公式是:sin(α+β)=sinαcosβ+cosαsinβ。sin(α-β)=sinαcosβ-cosαsinβ。记忆方式:异名同号。正弦的展开肯定就是以正弦开头,然后满足异名,正弦配余弦,符号就和我们要求的符号相同。
3、利用正弦函数的定义,我们知道正弦值等于对边长度与斜边长度的比值。

怎么推导正弦和余弦函数的公式啊?
1、平方公式:sinx=±√(1-cosx∧2)cosx=±√(1-sinx∧2)。诱导公式:sin(π/2+x)=cosx,cos(π/2+x)=—sinx。证明:sinx∧2+cosx∧2=1,移项得sinx∧2=1-cosx∧2,开平方得sinx=±√(1-cosx∧2)。
2、三角函数正弦公式为:sin(A) = 对边 / 斜边,余弦公式为:cos(A) = 邻边 / 斜边。正弦公式 正弦公式是 sin(x) = 对边 / 斜边,也可以表示为 sin(x) = b / c。
3、正弦函数 sin(A)=a/c 余弦函数 cos(A)=b/c 正切函数 tan(A)=a/b 余切函数 cot(A)=b/a 其中a为对边,b为临边,c为斜边,通常的三角函数是在平面直角坐标系中定义的。
4、正弦余弦函数的推导:正弦函数定义为“对边”与斜边之比,即sin(θ)=y/c。由于c=x+y,因此sin(θ)=y/c=(y)/(x+y)。

5、sinx泰勒公式:sinx=sinα·cosβ。sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
到此,以上就是小编对于正弦函数如何推导过来的的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏