本篇目录:
正切公式怎样推导的
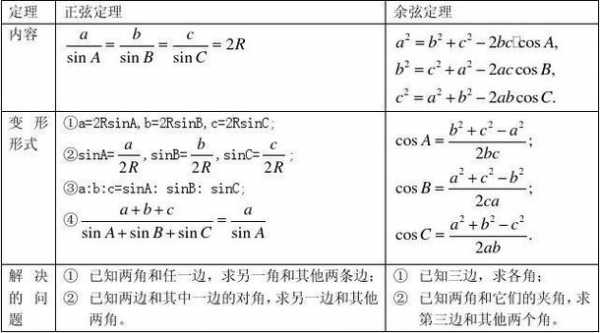
两角和正切公式为tan(A+B)=(tanA+tanB)/(1-tanAtanB)。
推导:tan2A=tan(A+A)=(tanA+tanA)/(1-tanAtanA)=2tanA/[1-(tanA)^2] 半角公式 利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。

两直线夹角的正切值公式可以通过向量的点积来推导得出。假设有两条直线 L1 和 L2,它们的斜率分别为 m1 和 m2,并且它们之间的夹角为 θ。 首先,计算两条直线的方向向量。
先利用单位圆(向量)推到两角和与差的余弦公式,再利用诱导公式推导正弦公式,最后利用同角三角函数的基本关系推到正切公式。
三角函数常用正切公式:tanb=sinb/cosb tan(a+b)=(tana+tanb)/(1-tana*tanb)注:若是a-b,则把后面的加减都换一下。
正切和差公式1:tan(a ± b) = (tan(a) ± tan(b)) / (1 tan(a)tan(b)) 正切和差公式2:tan(a ± b) = (sin(a ± b)) / (cos(a ± b))这两个公式可以互相推导得到。
三角函数公式推导过程
1、三角函数的推导过程是建立直角三角形坐标系、利用勾股定理推导、正弦余弦函数的推导。建立直角三角形坐标系:为了推导三角函数,我们需要在直角三角形中建立一个坐标系。以直角顶点为原点,水平方向为x轴,垂直方向为y轴。
2、具体步骤如下: 利用和差化积公式把三角函数表示成一个或多个三角函数的积,例如 sin(x + y) = sin(x)cos(y) + cos(x)sin(y)。
3、三角函数万能公式推导过程是设tan(A/2)=t,sinA=2t/(1+t^2),tanA=2t/(1-t^2),cosA=(1-t^2)/(1+t^2)。当要求一串函数式最值的时候就可以用万能公式。
4、三角函数公式推导的过程如下:aSINA=bSinB a/SinA=b/SinB so a^2=b^2 a=b。

5、分别由左右两边实部和虚部相等,可以推导出n倍角余弦和正弦三角函数公式。
正切余弦正弦关系公式
1、正切tanA=对边/邻边,余弦cosA=邻边/斜边,正弦sinA=对边/斜边。正切 在Rt△ABC(直角三角形)中,∠C=90°,AB是∠C的对边c,BC是∠A的对边a,AC是∠B的对边b,正切函数就是tanB=b/a,即tanB=AC/BC。
2、正弦余弦正切公式为sinα=tanαcosαcosα=cotαsinα,tanα=sinαsecαcotα=cosαcscα,secα=tanαcscαcscα=secαcotα。
3、正弦(sin):角α的对边比上斜边。余弦(cos):角α的邻边比上斜边。
4、正弦值(Sine,缩写为 sin):正弦值是对边与斜边之比,即 sin(θ) = 对边 / 斜边。余弦值(Cosine,缩写为 cos):余弦值是邻边与斜边之比,即 cos(θ) = 邻边 / 斜边。
5、正弦余弦正切的关系:sinA/cosA=tanA,三角函数是基本初等函数之一,是以角度为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。
6、sin和cos的关系有:sinα+cosα=1;sinx=cos(90-x);tanα=sinα/cosα;sin平方α*cos平方α=1。sinα是正弦,cosα是余弦。
三角函数公式的推导过程是怎样的?
1、三角函数的推导过程是建立直角三角形坐标系、利用勾股定理推导、正弦余弦函数的推导。建立直角三角形坐标系:为了推导三角函数,我们需要在直角三角形中建立一个坐标系。以直角顶点为原点,水平方向为x轴,垂直方向为y轴。
2、三角函数的推导过程主要基于直角三角形和单位圆的几何关系。以下为推导过程:正弦函数的推导 单位圆的定义:在平面直角坐标系中,以原点为圆心,半径为1的圆称为单位圆。
3、推导方法如下:定名法则 90°的奇数倍+α的三角函数,其绝对值与α三角函数的绝对值互为余函数。90°的偶数倍+α的三角函数与α的三角函数绝对值相同。也就是“奇余偶同,奇变偶不变”。
4、具体推导:首先建立直角坐标系,在直角坐标系xOy中作单位圆O,并作出角a,b,与-b,使角a的开边为Ox,交圆O于点P1,终边交圆O于点P2,角b的始边为OP2,终边交圆O于点P3,角-b的始边为OP1,终边交圆O于点P4。
5、三角函数万能公式推导过程是设tan(A/2)=t,sinA=2t/(1+t^2),tanA=2t/(1-t^2),cosA=(1-t^2)/(1+t^2)。当要求一串函数式最值的时候就可以用万能公式。
6、三角函数公式推导三角函数公式推导的过程如下:aSINA=bSinB a/SinA=b/SinB so a^2=b^2 a=b。
到此,以上就是小编对于正余弦正切定理的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏