本篇目录:
hl定理的证明过程
证明两直角三角形全等的条件:两个直角三角形的一条斜边与一条直角边分别对应相等,则两个直角三角形全等,简称HL。记住:前提是一定要是直角三角形(Rt),可以和SSS转化。hl证明三角形全等是直角边和斜边。
证明:直角三角形HL判定定理的内容是:两个直角三角形的一条直角边和斜边分别对应相等,则这两个直角三角形全等。

HL定理是证明两个直角三角形全等的定理,通过证明两个直角三角形斜边和直角边对应相等来证明两个三角形全等。判定定理为:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等(简记为HL)。
HL是证明两个直角三角形全等的定理,通过证明两个直角三角形斜边和直角边对应相等来证明两个三角形全等。前提是一定要是直角三角形(Rt),可以和SSS转化。
直角三角形证明全等的方法hl
1、ASA(角边角),即三角形的其中两个角对应相等,且两个角夹的的边也对应相等的两个三角形全等。AAS(角角边),即三角形的其中两个角对应相等,且对应相等的角所对应的边也对应相等的两个三角形全等。
2、关于直角三角形全等判定hl如下:直角三角形两直角边的平方和等于斜边的平方。∠BAC=90°,则AB+AC=BC。在直角三角形中,两个锐角互余。直角三角形中,斜边上的中线等于斜边的一半。该性质称为直角三角形斜边中线定理。
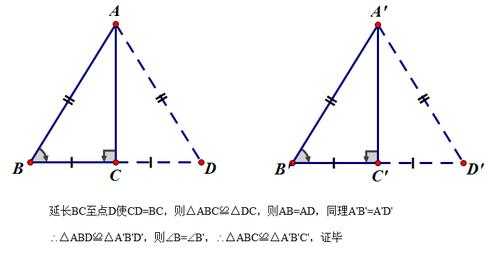
3、方法HL是证明两个直角三角形全等的定理,即在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等。除了HL之外,还可以用SSS、SAS、ASA、AAS来证明两个三角形全等。
HL定理证明(详细一点,因为不太会用勾股定理)
1、证明两直角三角形全等的条件:两个直角三角形的一条斜边与一条直角边分别对应相等,则两个直角三角形全等,简称HL。记住:前提是一定要是直角三角形(Rt),可以和SSS转化。hl证明三角形全等是直角边和斜边。
2、记住:前提是一定要是直角三角形(Rt)。H是(斜边)的缩写,L是(直角边)的缩写。
3、直角三角形hl定理如下:直角三角形两直角边的平方和等于斜边的平方。∠BAC=90°,则AB+AC=BC(勾股定理)。在直角三角形中,两个锐角互余。

到此,以上就是小编对于hl怎么求证的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏