本篇目录:
怎么判断凸函数和凹函数?如何证明?
若f(x) ≥ 0,则函数为凹函数;若f(x) ≤ 0,则函数为凸函数。
如果一个函数在某个区间内的二阶导数大于0,那么这个函数在这个区间内是凹函数。这意味着函数图像是向下凸出的。如果一个函数在某个区间内的二阶导数小于0,那么这个函数在这个区间内是凸函数。
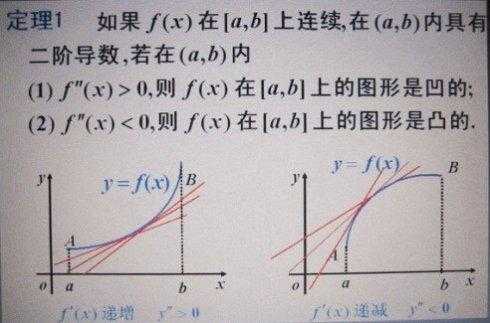
函数的凹凸性判断方法:若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凹的;若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凸的。
在函数f(x)的图像上取任意两点,如果函数图像在这两点之间的部分总在连接这两点的线段的下方,那么这个函数就是凹函数。直观上看,凸函数就是图像向上凸出来的。
凹凸函数的判断方法如下:设函数f(x)在区间I上连续,在区间内任取两点x1和x2,如果对于区间上任意两点x1及x2,当x1x2时,恒有f(x1)f(x2),则称函数f(x)在区间I上是凹函数。
凹函数定义:设函数y =f (x ) 在区间I 上连续,对x 1, x 2∈I ,若恒有f (则称y =f (x ) 的图象是凹的,函数y =f (x ) 为凹函数。
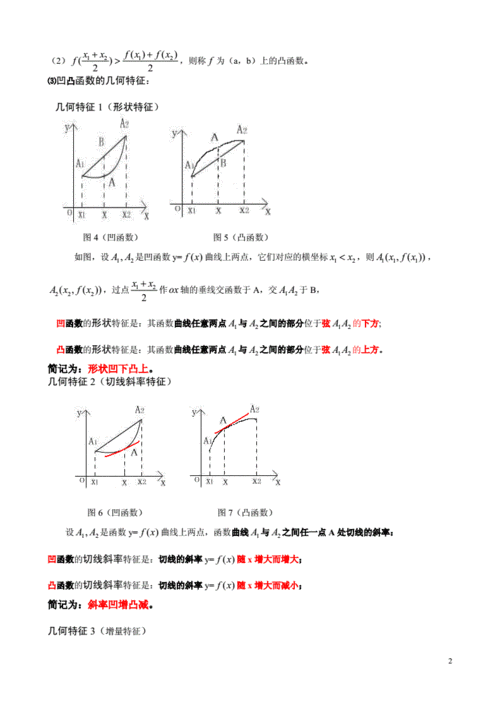
如何判断一个函数是凹函数还是凸函数
函数的凹凸性判断方法:若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凹的;若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凸的。
二阶导数大于0则原函数为凹函数,小于0为凸函数。设f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数,那么:(1)若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凹的。
要判断一个函数的凹凸性,我们需要考虑函数的二阶导数。一般来说,若函数的二阶导数在某个区间内恒大于等于零,则该函数在该区间内为凹函数;若函数的二阶导数在某个区间内恒小于等于零,则该函数在该区间内为凸函数。
如果一个函数在某个区间内的二阶导数大于0,那么这个函数在这个区间内是凹函数。这意味着函数图像是向下凸出的。如果一个函数在某个区间内的二阶导数小于0,那么这个函数在这个区间内是凸函数。
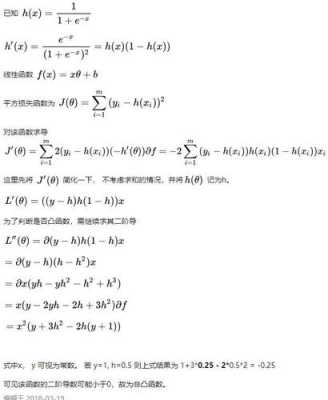
函数凹凸性的判断方法是:看导数,代数上,函数一阶导数为负,二阶导数为正(或者一阶正,二阶负),便是凸的,一阶与二阶同号为凹。函数在凹凸性发生改变的点称为拐点,拐点的二阶导数为0或不存在二阶导数。
凹凸函数的判定方法:在图像上任取两点A、B连接,若函数图像在两点间的部分均在直线下方,则把该函数在[A,B]之间的部分定义为凹函数。反正为凸函数。
凹函数怎么证明?
1、f(λx1+(1-λ)x2)=λf(x1)+(1-λ)f(x2),则称f为I上的凹函数.若不等号严格成立,即“”号成立,则称f(x)在I上是严格凹函数。
2、在图像上任取两点A、B连接,若函数图像在两点间的部分均在直线下方,则把该函数在[A,B]之间的部分定义为凹函数。反正为凸函数。
3、函数凹凸性的判断方法是:看导数,代数上,函数一阶导数为负,二阶导数为正(或者一阶正,二阶负),便是凸的,一阶与二阶同号为凹。函数在凹凸性发生改变的点称为拐点,拐点的二阶导数为0或不存在二阶导数。
4、函数的凹凸性判断方法:若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凹的;若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凸的。
如何证明一个函数是凹或凸函数?
(1)若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凹的。(2)若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凸的。
函数的凹凸性判断方法:若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凹的;若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凸的。
若f(x) ≥ 0,则函数为凹函数;若f(x) ≤ 0,则函数为凸函数。
如果一个函数在某个区间内的二阶导数大于0,那么这个函数在这个区间内是凹函数。这意味着函数图像是向下凸出的。如果一个函数在某个区间内的二阶导数小于0,那么这个函数在这个区间内是凸函数。
凹函数性质证明
凹函数的性质介绍如下:函数的导函数单调递增。也就是说,如果f(x)是一个凹函数,则f’(x)在定义域上单调递增。凸函数的二阶导数大于等于0。也就是说,如果f(x)是一个凹函数,则f(x)在定义域上大于等于0。
所谓拟凹函数,就是相对坐标横轴,图像里没有下凸现象的曲线。亦即对任意两点x、y属于定义域,f(ax+(1-a)y)=min[f(x), f(y)]。
凹凸函数的性质:即函数图像是向上凸还是向下凸。
函数的凹凸性是描述函数图像弯曲方向的一个重要性质,其应用也是多方面的。
f(q1x1+q2x2)≥q1f(x1)+q2f(x2),其中qq2为正数,q1+q2=1恒成立。凹函数图像如下。
则f称为I上的凹函数。拟凹函数,就是相对坐标横轴,图像里没有下凸现象的曲线。亦即对任意两点x、y属于定义域,f(ax+(1-a)y)=min[f(x), f(y)]。严格拟凹函数是凹函数的推广,保留了许多凹函数的性质。
用导数如何判断函数凹凸?
凹凸性判定记忆口诀为看导数,代数上,函数一阶导数为负,二阶导数为正(或者一阶正,二阶负),便是凸的,一阶与二阶同号为凹。函数在凹凸性发生改变的点称为拐点,拐点的二阶导数为0或不存在二阶导数。
要判断一个函数的凹凸性,我们需要考虑函数的二阶导数。一般来说,若函数的二阶导数在某个区间内恒大于等于零,则该函数在该区间内为凹函数;若函数的二阶导数在某个区间内恒小于等于零,则该函数在该区间内为凸函数。
函数凹凸性的判断方法是:看导数,代数上,函数一阶导数为负,二阶导数为正(或者一阶正,二阶负),便是凸的,一阶与二阶同号为凹。函数在凹凸性发生改变的点称为拐点,拐点的二阶导数为0或不存在二阶导数。
一般地,把满足[f(x1)+f(x2)]/2f[(x1+x2)/2]的区间称为函数f(x)的凹区间;反之为凸区间;凹凸性改变的点叫做拐点。
函数的凹凸性判断方法:若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凹的;若在(a,b)内f(x)0,则f(x)在[a,b]上的图形是凸的。
函数凹凸性的判断方法是看导数,代数上,函数一阶导数为负,二阶导数为正(或者一阶正,二阶负),便是凸的,一阶与二阶同号为凹。函数在凹凸性发生改变的点称为拐点,拐点的二阶导数为0或不存在二阶导数。
到此,以上就是小编对于凹函数的证明过程是什么的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏