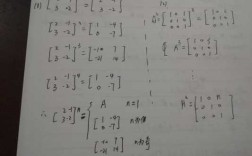本篇目录:
- 1、如何证明两个矩阵相似?
- 2、(K型)用相似比做
- 3、如何证明矩阵相似
如何证明两个矩阵相似?
1、矩阵相似的判定方法如下:特征值相同:两个矩阵相似的最重要特征是它们具有相同的特征值。也就是说,对于两个相似的矩阵A和B,它们的主对角线上的元素分别相等,且对应位置上的特征多项式相等。
2、判断两个矩阵是否相似的方法主要有以下几种:特征值法、行列式法、迹法、秩法。特征值法 如果两个矩阵的特征值相等,那么它们是相似的。这是因为矩阵在相似变换下是不变的。
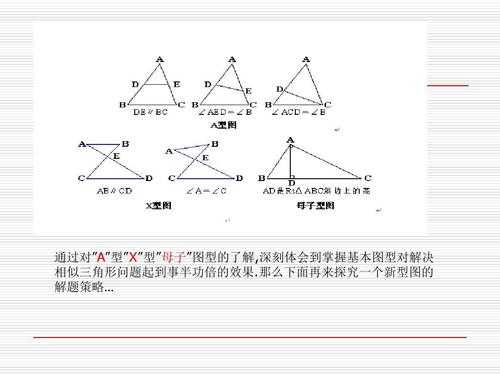
3、判断两个矩阵是否相似的方法有:01判断特征值是否相等。如果两个矩阵A和B的特征值相同,那么它们相似。特征值是矩阵的一个重要性质,它描述了矩阵在特定变换下的行为。
4、判断两个矩阵相似的方法是:判断特征值是否相等、判断行列式是否相等、判断迹是否相等、判断秩是否相等。两个矩阵相似充要条件是:特征矩阵等价行列式因子相同不变,因子相同初等因子相同,且特征矩阵的秩相同转置矩阵相似。
5、但是没有n个线性无关的特征向量也不行,只有D满足条件。充分条件是有n个线性无关的特征向量。判断两个矩阵相似的辅助方法:判断特征值是否相等;判断行列式是否相等;判断迹是否相等;判断秩是否相等。
6、证明:设矩阵a与b相似,fa(x),fb(x)分别为它们的最小多项式。由a相似于b,存在可逆矩阵T,使b=TaT。
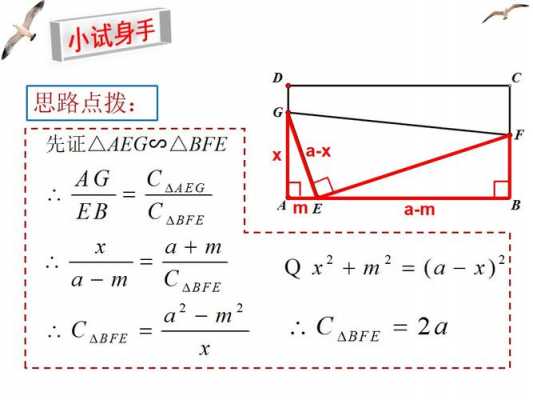
(K型)用相似比做
k是相似比 若问怎么得来的,那就是条件和结果的关系了。我想你也是明白的 1)已知abcd和a1b1c1d1相似,相似比=k 2)知道四边形三个内角相等。。
位似比,即位似图形的相似比,指的是新图形与参照的原图形之间的相似比。位似图形:如果两个相似图形的每组对应顶点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形。
不可以。因为“相似比”的概念是对于两个相似三角形而言的。不过,有关比例线段的比例式是可以按自身的边比自身的边来写出的。
如何证明矩阵相似
1、证明:设矩阵a与b相似,fa(x),fb(x)分别为它们的最小多项式。由a相似于b,存在可逆矩阵T,使b=TaT。
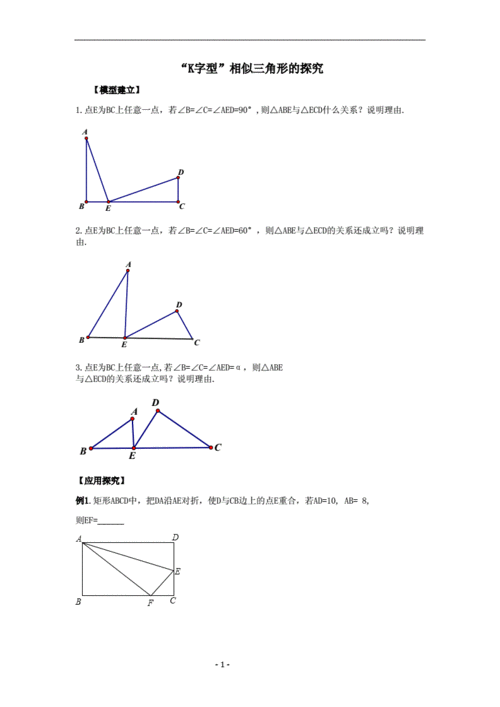
2、相似矩阵具有相同的可逆性,当它们可逆时,则它们的逆矩阵也相似。对称性:有A~B则有B~A。若A与对角矩阵相似,则称A为可对角化矩阵,若n阶方阵A有n个线性无关的特征向量,则称A为单纯矩阵。
3、都可以对角化就说明都与对角阵相似,且特征值相同,说明和同一对角阵相似,由相似的传递性可知,A B相似。在线性代数中,相似矩阵是指存在相似关系的矩阵。
4、如何证明两个矩阵相似如下:先求解两矩阵特征值相同。再证明两矩阵均可相似对角化。
5、相似的定义为:对n阶方阵A、B,若存在可逆矩阵P,使得P^(-1)AP=B,则称A、B相似。
6、判断矩阵A,B是否相似的步骤:1,判断A,B的特征值及重数是否完全相同。不相同不相似,相同则第2步,判断A,B是否都可相似对角化,都可对角化,AB相似。一个可以相似对角化一个不可以,那么AB不相似。
到此,以上就是小编对于k形相似是什么意思的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏