本篇目录:
费马大定理证明过程是怎么样的?
1、费马定理的证明过程如下:1,热尔曼证明了当n和2n+1都是素数时,费马大定理的反例x,y,z至少有一个是n整倍数。
2、费马大定理的证明过程:费马大定理证明过程:设:a=d^(n/2),b=h^(n/2),c=p^(n/2);则a^2+b^2=c^2就可以写成d^n+h^n=p^n,n=3……当n=1 时,d+h=p,d、h与p可以是任意整数。
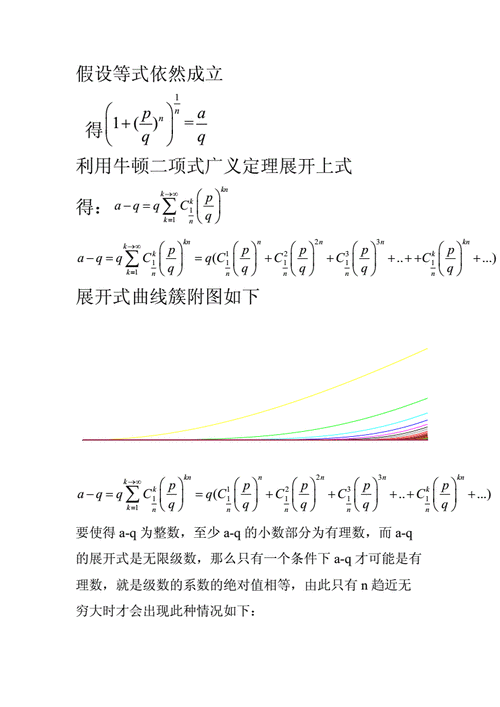
3、费马大定理的证明方法:x+y=z有无穷多组整数解,称为一个三元组;x^2+y^2=z^2也有无穷多组整数解,这个结论在毕达哥拉斯时代就被他的学生证明,称为毕达哥拉斯三元组,我们中国人称他们为勾股数。
4、至此费马大定理得证。怀尔斯和他以前的博士研究生理查德泰勒用了近一年的时间,用之前一个怀尔斯曾经抛弃过的方法修补了这个漏洞,这部份的证明与岩泽理论有关。这就证明了谷山-志村猜想,从而最终证明了费马大定理。
5、费马大定理:对费马方程x^n+y^n=z^n整数解关系的证明,多年来在数学界一直颇多争议。本文利用平面几何方法,全面分析了直角三角形边长a^2+b^2=c^2整数解的存在条件,提出对多元代数式应用增元求值。
费马大定理的证明
费马大定理(Fermats Last Theorem)是指当n为正整数且大于2时,方程a^n + b^n = c^n没有正整数解。

假若d、h、p可以以整数的形式出现,说明等式d^n+h^n=p^n成立,费马大定理不成立。否则,d^n+h^n≠p^n不等式成立,费马大定理成立。
费马中值定理公式:利用连续函数在闭区间的介值定理可解决的一类中值问题,即证明存在ξ∈[a,b],使得某个命题成立。
费马大定理的证明过程是复杂且深奥的,涉及多个领域的知识。
费马大定理证明过程:设:a=d^(n/2),b=h^(n/2),c=p^(n/2);则a^2+b^2=c^2就可以写成d^n+h^n=p^n,n=3……当n=1时,d+h=p,d、h与p可以是任意整数。

费马大定理的证明过程
费马定理的证明过程如下:1,热尔曼证明了当n和2n+1都是素数时,费马大定理的反例x,y,z至少有一个是n整倍数。
.x+y=z有无穷多组整数解,称为一个三元组;x^2+y^2=z^2也有无穷多组整数解,这个结论在毕达哥拉斯时代就被他的学生证明,称为毕达哥拉斯三元组,我们中国人称他们为勾股数。
验证:当m=±1时,b=h^(n^2)=(m^2-1)^2=0;即a^2=c^2。与题要求不符。假若d、h、p可以以整数的形式出现,说明等式d^n+h^n=p^n成立,费马大定理不成立。
费马大定理证明是什么?
1、费马定理的证明过程如下:1,热尔曼证明了当n和2n+1都是素数时,费马大定理的反例x,y,z至少有一个是n整倍数。
2、假若d、h、p可以以整数的形式出现,说明等式d^n+h^n=p^n成立,费马大定理不成立。否则,d^n+h^n≠p^n不等式成立,费马大定理成立。
3、费马中值定理公式:利用连续函数在闭区间的介值定理可解决的一类中值问题,即证明存在ξ∈[a,b],使得某个命题成立。
4、费马大定理的证明过程是数学逻辑的完美体现,它涉及了数论、代数和几何等多个数学领域,并推动了这些领域的发展。在费马大定理的证明过程中,我们可以看到数学思维的严谨性和深刻性,这使得它成为了数学史上的经典之作。
5、费马定理证明就是运用费马定理去证明等式,费马大定理,别称费马猜想、费马最后的定理,是指当整数n2时,关于x,y,z的方程x^n+y^n=z^n没有正整数解。费马大定理被提出后,经历多人猜想辩证。
6、费马大定理(Fermats Last Theorem)是指当n为正整数且大于2时,方程a^n + b^n = c^n没有正整数解。
求费马大定理的全部证明过程!!!
1、费马大定理: 当整数n 2时,关于x, y, z的不定方程 x^n + y^n = z^n. 无正整数解。 费马矩阵大定理:当整数n 2时,关于m行m列矩阵X, Y, Z的不定矩阵方程 X^n + Y^n =Z^n. 矩阵的元素中至少有一个零。
2、费马定理的证明过程如下:1,热尔曼证明了当n和2n+1都是素数时,费马大定理的反例x,y,z至少有一个是n整倍数。
3、假若d、h、p可以以整数的形式出现,说明等式d^n+h^n=p^n成立,费马大定理不成立。否则,d^n+h^n≠p^n不等式成立,费马大定理成立。
到此,以上就是小编对于费马定理的证明过程是的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏