本篇目录:
- 1、三角函数所有求导公式总结
- 2、余弦的导数如何求
- 3、sinx的导数及推导过程
- 4、三角函数的导数公式大全
- 5、三角函数导数推导过程
- 6、函数求导公式及推导过程
三角函数所有求导公式总结
正弦函数求导:正弦函数的一般形式是y= sin(x),其中x是角罩迅衫度(以弧度为单位)。正弦函数的导数是:y=cos(x)。正弦函数在一个周期内的图形是一个波浪形,其斜率在每个周期内都在变化。
三角函数求导公式有:tanα·cotα=1,sinα·cscα=1,cosα·secα=1,sinα/cosα=tanα=secα/cscα,cosα/sinα=cotα=cscα/secα,sin2α+cos2α=1,1+tan2α=sec2α,1+cot2α=csc2α等。
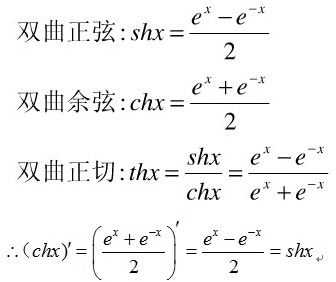
三角函数求导公式包括y=c(c为常熟),导函数是y=0;指数函数y=ex的导函数是y=axlna等。
余弦的导数如何求
(cosx)^2-(sinx)^2=1-(sinx)^2-(sinx)^2=1-2(sinx)^2=cos2x。余弦(余弦函数),三角函数的一种。
余弦函数的导数是:y=-sin(x)。余弦函数的图形与正弦函数类似,也是一个波浪形,但其斜率与正弦函数相反。因此,余弦函数的导数是负的正弦函数的导数。
函数值域的限制:反三角函数的定义域通常有限制。例如,反正弦函数(arcsin)的定义域为-1到1,反余弦函数(arccos)的定义域为0到1,反正切函数(arctan)的定义域为所有实数。

sinx的导数及推导过程
1、sinx的导数是cosx(其中x为变量),sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
2、cosx的导数是-sinx。即y=cosx y=-sinx。证明过程:用和差化积公式cos(a) - cos(b) = - 2sin[(a+b)/2]sin[(a-b)/2]。重要极限lim(h-0) sin(h)/h = 1。
3、sinx=[e^(ix)-e^(-ix)]/(2i)。高等代数中三角函数的指数表示(由泰勒级数易得):sinx=[e^(ix)-e^(-ix)]/(2i) 。cosx=[e^(ix)+e^(-ix)]/2 。
4、sinx是正弦函数,而cosx是余弦函数,两者导数不同,sinx的导数是cosx,而cosx的导数是 -sinx,这是因为两个函数的不同的单调区间造成的。
5、sinX的导数是cosX,而cosX的导数是 -sinX。
6、y=tanx y=1/cos^2x y=cotx y=-1/sin^2x y=arcsinx y=1/√1-x^2 导数的求导法则 由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。
三角函数的导数公式大全
1、三角函数求导公式有:tanα·cotα=1,sinα·cscα=1,cosα·secα=1,sinα/cosα=tanα=secα/cscα,cosα/sinα=cotα=cscα/secα,sin2α+cos2α=1,1+tan2α=sec2α,1+cot2α=csc2α等。
2、三角函数求导公式包括y=c(c为常熟),导函数是y=0;指数函数y=ex的导函数是y=axlna等。
3、三角函数求导公式:(sinx)=cosx、(cosx)=-sinx、(tanx)=secx=1+tanx。三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。
4、(4)高阶导数的递推公式 对于一些特殊函数,可以通过递推关系来计算高阶导数。例如,指数函数的n阶导数仍然是指数函数,三角函数的n阶导数可以通过递推公式来计算。
三角函数导数推导过程
三角函数求导公式:(sinx)=cosx、(cosx)=-sinx、(tanx)=secx=1+tanx。三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。
解答过程如下:(1)设u=tanx,则tanx可以表示成u。
正弦函数的导数:f(x)=cos(x),其中f(x)=sin(x)。解释:正弦函数的导数可以根据三角函数的求导法则进行推导。根据三角函数的求导法则,我们可以得到(sinx)=cosx。
函数求导公式及推导过程
个基本导数公式推导过程如下:y=c,y=0(c为常数)。y=x^μ,y=μx^(μ-1)(μ为常数且μ≠0)。y=a^x,y=a^xlna;y=e^x,y=e^x。
y=a^x,△y=a^(x+△x)-a^x=a^x(a^△x-1),△y/△x=a^x(a^△x-1)/△x。如果直接令△x→0,是不能导出导函数的,必须设一个辅助的函数β=a^△x-1通过换元进行计算。
常数函数的导数:对于任意常数c,导数为0。推导过程:根据导数的定义,我们有f(x) = lim(h-0) [f(x+h) - f(x)]/h。
到此,以上就是小编对于余弦函数导数推导过程图的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏