本篇目录:
极坐标系下二重积分公式怎么推导的呢?
1、对于平面内任何一点M,用ρ表示线段OM的长度(有时也用r表示),θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对 (ρ,θ)就叫点M的极坐标,这样建立的坐标系叫做极坐标系。
2、可以先用微元法得到二重积分,然后将 ρ,θ看做新的变量X与Y,再利用直角坐标系来计算可以得到二次积分的表达式,这个应该好理解些吧。

3、r 的积分限确定方法:从极点出发一条射线,射线穿过积分区域D,先穿过的曲线φ1(θ)为积分下限,后穿过的曲线φ2(θ)为积分上限。
极坐标的公式怎么推导出来的?
另一种做法是用一般函数图形绕x轴旋转的旋转体体积公式,换元x=rcosθ,y=rsinθ即可得到此公式。
利用公式:x=ρcosθ,y=ρsinθ,直接将x和y作代换后代入原方程,即可将直角坐标方程化为极坐标方程。
首先,我们注意到 $\tan\theta = \frac{y}{x}$,所以有 $\theta = \arctan\frac{y}{x}$。

极坐标面积公式=∫2πyds=∫2πrsinθ√(r^2+r^2)dθ,wheresisarclength。
首先对极径r进行积分,得到整个圆环内的总质量;然后对极角θ进行积分,得到整个圆环内的质量分布情况。最后将两者相乘,就得到了该区域内的面积或体积。由于极坐标系的特殊性质,该公式中的dxdy需要被替换为rdrdθ。
极坐标公式怎么推导的?
极坐标面积公式=∫2πyds=∫2πrsinθ√(r^2+r^2)dθ,wheresisarclength。
极坐标下的二重积分公式推理过程如下:过程 假设平面上的区域由两个函数f(x,y)和g(x,y)所确定,其中f(x,y)表示该区域内的密度分布函数,g(x,y)表示该区域内的高度分布函数。
极坐标曲线弧长公式推导:假设极坐标曲线的方程为r=f(θ),其中r表示极径,θ表示极角。我们需要计算从θ1到θ2的一段弧长L。为了计算弧长,我们可以将曲线分成许多小段,每一小段的长度可以近似为直线段的长度。
选择合适的极坐标形式:根据图形的形状和特征选择适当的极坐标形式。例如,对于圆形或部分圆形,可以使用 r=a 或 r=f(θ) 的形式;对于螺线,可以使用 r=aθ 或 r=f(θ) 的形式。
过这个点作直径,交圆于Q连接OQ、OP,就有直角三角形POQ,然后再利用角度之间相等的关系来做。
极坐标公式怎么推导?
圆的极坐标公式:ρ=x+y,x=ρcosθ,y=ρsinθ,tanθ=y/x,(x不为0)。在数学中,极坐标系是一个二维坐标系统,该坐标系统中任意位置可有一个夹角和一段相对原点—极点的距离来表示。
极坐标面积公式=∫2πyds=∫2πrsinθ√(r^2+r^2)dθ,wheresisarclength。
极坐标曲线弧长公式推导:假设极坐标曲线的方程为r=f(θ),其中r表示极径,θ表示极角。我们需要计算从θ1到θ2的一段弧长L。为了计算弧长,我们可以将曲线分成许多小段,每一小段的长度可以近似为直线段的长度。
极坐标下的二重积分公式推理过程如下:过程 假设平面上的区域由两个函数f(x,y)和g(x,y)所确定,其中f(x,y)表示该区域内的密度分布函数,g(x,y)表示该区域内的高度分布函数。
如何求出极坐标方程?
1、利用公式:x=ρcosθ,y=ρsinθ,直接将x和y作代换后代入原方程,即可将直角坐标方程化为极坐标方程。
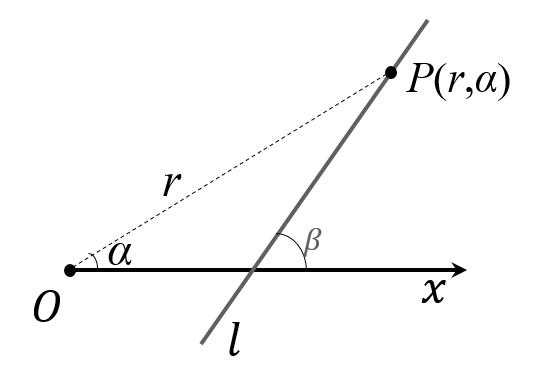
2、设直线方程为 ax+by+c=0,在极坐标系中x=rsinθ,y=rcosθ,代入可得aρcosθ+bρsinθ+c=0。
3、圆的极坐标方程6个公式:ρ=x+y,x=ρcosθ,y=ρsinθ,tanθ=y/x,ρ=2Rcosθ,ρ-2Rρ(sinθ+cosθ)+R=0。
4、要确定一个极坐标方程,可以按照以下步骤进行: 确定极坐标中心:确定极坐标的原点 (r=0) 所在的位置。这通常可以通过图形上的信息或给定条件得出。
5、首先来把极坐标方程中的坐标θ去整理成cosθ和sinθ的形式 ;如下图所示一样。接下来:再把坐标cosθ化成x/ρ,再把sinθ化成y/ρ,也可以把ρcosθ化成x,把ρsinθ化成y,这样就更方便和直接理解。
6、要从直角坐标系转换为极坐标系,需要以下两个步骤:计算极径(r):极径是点到原点的距离,可以使用勾股定理计算。
极坐标公式是什么意思?如何推导?
极坐标是指在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向)。
圆的极坐标公式:ρ=x+y,x=ρcosθ,y=ρsinθ,tanθ=y/x,(x不为0)。在数学中,极坐标系是一个二维坐标系统,该坐标系统中任意位置可有一个夹角和一段相对原点—极点的距离来表示。
极坐标公式是什么?x = rcos(θ),y = rsin(θ),r^2=x^2+y^2 (一般默认r0),tan(θ)=y/x (x≠0)。在数学中,极坐标系是一个二维坐标系统。
椭圆的极坐标方程公式:r=a(1-e)/(1-ecosθ)。在数学中,极坐标系是一个二维坐标系统。该坐标系统中任意位置可由一个夹角和一段相对原点—极点的距离来表示。
到此,以上就是小编对于极坐标矢量运算的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏