本篇目录:
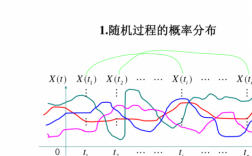
随机信号的随机过程
随机过程属于随机信号。通信中的信号和噪声都具有一定的随机性,需要用随机过程的理论来描述。随机过程可以定义为所有样本函数的集合。
从信号分析的角度来说,随机信号和噪声都是随机过程。随机过程是一笼统的概念,平常指的是随机过程的任一实现。

由此可见,随机信号所发生的物理过程是一个随机过程,它是一个时间函数集,通常认为是具有无限长度和无限能量的功率信号。
随机信号是随机过程,其每个时间点都是一个随机变量。如同你学概率论提到的 随机变量没有值的说法,它只有观测值,也就是说你对随机变量进行一次测量会得到一组值。
随机信号的特征参数:随机信号的主要特征参数是:均值、均方值、方差、概率密度函数、相关函数和功率谱密度函数来描述随机过程的特性 功率谱是描述随机信号基本特征的重要参数。
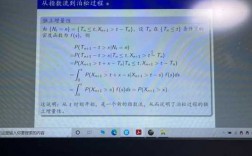
简述更新过程与泊松过程的区别与联系
较泊松过程稍为广泛的计数过程是更新过程,更新过程的跳跃时间间距是相互独立同分布的,但不一定是指数分布。这类过程常被用来描写某些设备的累计故障次数。

生灭过程和泊松过程的区别是过程不同。生灭过程,是一种特殊的离散状态的连续时间马尔可夫过程,或被称为连续时间马尔可夫链。
更新过程是泊松过程的推广,其事件(更新)发生的时间间隔仍为独立同分布但不要求是指数分布。更新过程不再是平稳独立增量过程。举例说明。
区别:泊松过程是一类较为简单的时间连续状态离散的随机过程。复合泊松过程是由对泊松过程的每一点赋予一独立同分布的随机变量而得的随机过程。
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。泊松分布P(λ)中只有一个参数λ ,它既是泊松分布的均值,也是泊松分布的方差。

任意持有时间,概率论的分支是理论更新。更新理论是将泊松过程概括为任意持有时间,是概率论的分支,应用包括计算工厂中更换破旧机械的最佳策略,保险单的长期效益等,更新过程是类随机过程,是描述元件和设备更新现象的随机过程。
随机过程的基本概念
1、所以,随机过程就是一个以时间为线索的随机变量的集合。在随机过程{ X(t), t}中,如果固定时刻t,即观察随机过程中的一个随机变量。
2、学习基本概念:学习随机过程的基本概念,包括概率空间、样本空间、随机变量、概率密度函数、概率分布函数等。学习不同类型的随机过程:随机过程可以分为离散型随机过程和连续型随机过程。
3、随机变量是指在同一条件下,事件每次发生的结果是随机的、不确定的,而随机过程是指在同样条件下,事物发生的某一过程是随机的、不可准确预知的。
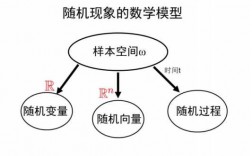
概率,随机变量,随机过程
在 概率论 中 , 通常研究 一个或多个这样有限个数 的随机变量,即使在大数定律和中心极限定理中考虑了无穷多个随机变量,但也要假设随机变量之间 互相独立。
概率论是数学的一个分支,主要研究随机现象的规律性。概率论的基本概念包括随机事件、样本空间、概率,条件概率等。随机事件是指在一定条件下可能发生,也可能不发生的事件。
学习基本概念:学习随机过程的基本概念,包括概率空间、样本空间、随机变量、概率密度函数、概率分布函数等。学习不同类型的随机过程:随机过程可以分为离散型随机过程和连续型随机过程。
括概率与随机变量、随机过程、随机变量与随机过程在信号处理和通信中的应用三部分。
应用随机过程复习资料
该习题集的内容包括随机过程的定义、性质、估计和预测等方面,涵盖了随机过程的各个领域。其中,一些习题涉及到经典的随机过程模型,如马尔科夫链、泊松过程和布朗运动等。
https://pan.baidu.com/s/1lob90m3SFf2sYJSSLr3_ZQ?pwd=1234 《应用随机过程》一书主要对应用随机过程学的基础知识作了介绍,具体内容包括随机过程的基本概念和基本类型、Poisson过程、Markov链、Brown运动、随机积分等。
随机过程期末复习题库(2015)填空题对于具有常数均值的二阶矩过程数只与,为宽平稳过程当且仅当二元函有关,而与和无关。
随机过程及其在金融领域中的应用习题五答案如下:确定概率模型:首先需要明确问题是关于什么事件的概率,这个事件是由哪些基本事件构成的,以及每个基本事件的发生概率是多少。
到此,以上就是小编对于随机过程更新函数公式的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏