本篇目录:
- 1、数学体系
- 2、几何泊松过程可以用伊藤定理吗
- 3、统计学专业的课程有哪些
- 4、泊松分布到底是什么??麻烦说清楚,泊松事件呢?
- 5、什么是泊松过程?齐次泊松过程和非其次泊松过程又是什么?
- 6、泊松的后人评价
数学体系
数学知识的体系是很严密、精炼的。尤其是千挑万选用来引导初学者从无到有在各自的大脑里重新构建数学体系的教科书。前面的内容是后面的基础。就像架桥,先浇桥墩,然后才有支点可以安放桥身。
数学系统是是研究数学的历史、理论、方法、应用等的集理论与应用与一体的体系的统称。

解题能力也是知识体系的一部分,它所包含的内容有计算能力和题目分析能力,看到一道题目,能够快速把它与脑海中的模型题对应,找出题目的关键条件(突破口),分析出解题的路径,然后能够快速准确的把题目计算出来,解决掉。
实数系的完备化→数列的极限,函数的极限,连续性,可导性,微分与积分数项级数,函数项级数,级数展开多元微积分总之,当实数系建立了完备性以后,所有就可以牵成一条线了。
在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。为了适应时代发展对人才培养的需要,数学课程还要特别注重发展学生的应用意识和创新意识。
几何泊松过程可以用伊藤定理吗
考虑积分 如果我们简单应用微积分基本定理,有: 但是 ,所以, 微积分基本定理简单应用在伊藤意义下的随机积分中并不成立 。事实上,应用下面所述的伊藤公式,我们知道 (注意到这个等式的右边并不服从正态分布!)。

主要内容有随机变量、条件概率及条件期望、离散及连续马尔可夫链、指数分布、泊松过程、布朗运动及平稳过程、更新理论及排队论等;也包括了随机过程在物理、生物、运筹、网络、遗传、经济、保险、金融及可靠性中的应用。
平行轴定理(Steiner定理),转动惯量的相加性。(d)加速参考系,惯性力。不要求知道科氏力公式。流体力学 不专对这一部分出题,但希望学生知道压力、浮力、和连续定律的基本概念。
在代数方面,证明了历史长久遗留的一维射影几何的基本定理;给出了体的正规子体一定包含在它的中心之中这个结果的一个简单而直接的证明,被称为嘉当—布饶尔—华定理。
高中数学合集百度网盘下载 链接:https://pan.baidu.com/s/1znmI8mJTas01m1m03zCRfQ ?pwd=1234 提取码:1234 简介:高中数学优质资料下载,包括:试题试卷、课件、教材、视频、各大名师网校合集。
统计学专业的课程有哪些
1、金融数学,证券投资的统计分析,数值分析,数据结构与算法,数据库管理系统,计算机网络系统,系统分析与软件设计。专业课和主要基础课:数学分析、解析几何、高等代数、微分方程、复变函数、实变函数与泛函分析、近世代数。
2、统计学专业课程有微积分、多变量微积分、数据计算的概念、线性代数与微分方程、统计的概念等。微积分:它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。
3、统计学专业统计学方向 主干专业课 专业必修课:国民经济核算、多元统计分析、时间序列分析、抽样技术、应用统计软件、统计预测、统计决策、应用统计学、统计史。
泊松分布到底是什么??麻烦说清楚,泊松事件呢?
1、泊松分布:泊松分布适用于描述单位时间或单位面积内随机事件发生的次数。其特点是平均数等于方差,且当事件发生的概率较小、样本容量较大时,泊松分布可以近似地用于描述二项分布。
2、泊松分布是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松在1838年时发表。
3、泊松分布是一种离散概率分布,用于描述在固定时间或空间内事件发生的次数,假设事件之间是独立且平均发生率恒定的情况。历史背景:泊松分布由法国数学家西蒙·泊松于1837年提出。
4、泊松分布,也就是Poisson分布,是一种统计与概率学里常见到的离散概率分布。其概率函数为:P{X=k}=λ^k/(k!e^λ) k=0,1,2…k代表的是变量的值。
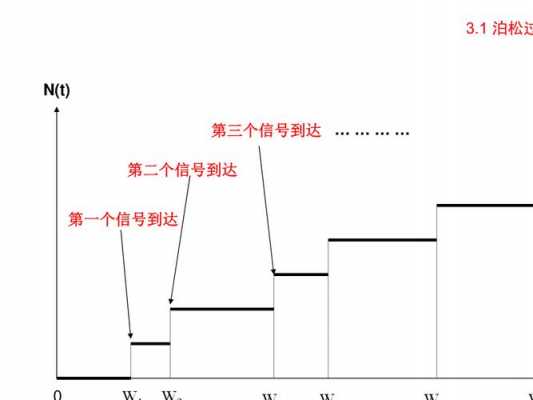
什么是泊松过程?齐次泊松过程和非其次泊松过程又是什么?
1、泊松过程是莱维过程(Lévy process)中最有名的过程之一。时间齐次的泊松过程也是时间齐次的连续时间Markov过程的例子。一个时间齐次、一维的泊松过程是一个纯出生过程,是一个出生-死亡过程的最简单例子。
2、非齐次泊松过程可通过时间尺度的变换变为齐次泊松过程。对泊松过程,通常可取它的每个样本函数都是跃度为1的左(或右)连续阶梯函数。
3、非齐次泊松过程可通过时间尺度的变换变为齐次泊松过程。对泊松过程,通常可取它的每个样本函数都是跃度为1的左(或右)连续阶梯函数。
4、泊松过程:泊松分布的概念还引申出了泊松过程。泊松过程是一种连续时间的随机过程,用于描述一系列相互独立的事件的发生。泊松过程在排队论、风险分析、金融模型等方面有重要应用。
5、泊松过程的性质包括: 到达间隔时间列{T,n=1,2,...}是独立同分布的指数随机变量,具有均值1/λ。这些性质使得泊松过程在数学建模和实际问题中有广泛的应用。
泊松的后人评价
在数学方面:美国数学史家克兰(Kline)指出:“泊松是第一个沿着复平面上的路径实行积分的人。”在他1817年的出版物中对序列收敛的条件就有了正确的概念,现在一般把这个条件归功于柯西。
激光打到不透明的圆盘上,使得圆盘的边缘各点相当于一组次级光源,其衍射的结果,在光屏上形成的圆盘阴影的中心有一个亮点,且阴影的边缘出现明暗相间的光环。这就是著名的泊松光斑。
由于这个亮斑是泊松首先计算出来的,后人就把它称为“泊松亮斑”。
到此,以上就是小编对于泊松过程课件的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏