本篇目录：

• 1、勾股定理推理过程是什么
• 2、勾股定理怎么推导的?
• 3、勾股定理的推导过程(最好是图示)
• 4、勾股定理怎么推导的
• 5、勾股定理的证明全过程
• 6、勾股定理是如何推导的?

勾股定理推理过程是什么

勾股定理是余弦定理的一个特例 证明 作△ABC≌△ABC使点A的对应点A在BC上，连接AA 、BB， 延长BA交AB于点M 。

勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理。

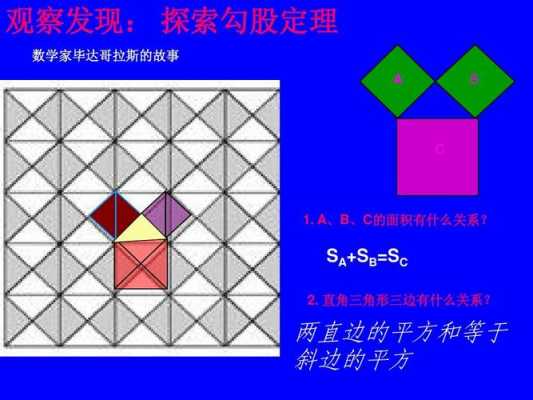
勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

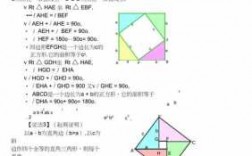
．中国方法 画两个边长为(a+b)的正方形，如图，其中a、b为直角边，c为斜边。这两个正方形全等，故面积相等。

探索勾股定理的过程，其实就是探索一个直角三角形，它三个边之间的关系。

勾股定理怎么推导的?

勾股定理基本公式：a+b=c（在直角三角形中，两个直角边分别为a和b；斜边为c)。勾股定理意义：1．勾股定理的证明是论证几何的发端。

都是用面积来进行验证：一个大的面积等于几个小面积的和。

那么，正方形OPEG的面积等于正方形ABCD的面积减去4个直角三角形的面积。即：c=(a＋b)－4×ab展开后得到，c=a＋b。

用向量的几何意义证明勾股定理，首先利用向量的长度和夹角的公式计算出向量的长度和夹角，再利用向量的点积公式计算出勾股定理中的各个变量，最后推导出勾股定理。割圆术证明法。

勾股定理的证明是论证几何的发端。勾股定理是历史上第一个把数与形联系起来的定理，即它是第一个把几何与代数联系起来的定理。勾股定理导致了无理数的发现，引起第一次数学危机，大大加深了人们对数的理解。

另一个是直角九十度。三角形的三条边中，如果一条边是三，另外一条边是四，还有一条边是五，也是适合勾股定理，在此基础上乘以2到n倍也是的，如3x2o二6o，4x2o＝8o，5x2o二1oo，达到了勾股定理标准。

勾股定理的推导过程(最好是图示)

我们可以用这三个小三角形的三角函数关系来证明勾股定理，具体步骤如下：第一步：画一个以A、B、C三个点为顶点的直角三角形ABC。[P]第二步 将点B往AC边上移动，得到一个新的点D。

勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

即“勾股各自乘，并之为弦实，开方除之，即弦也”。赵爽对勾股定理的证明，显示了我国数学家高超的证题思想，较为简明、直观。

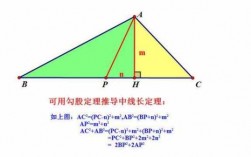
勾股定理：在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。

勾股定理怎么推导的

勾股定理3个公式a=k（m+n），b=2kmn，c=k（m+n）。勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。

证明如下：已知一个正方形ABCD，边长为a＋b，正方形ABCD各边各取一个点O、P、E、G，构成一个四边形OPEG。已知，BO=AP=DE=CG=a，OA=PD=EC=GB=b。

勾股定理的推导过程 勾股定理是由古希腊数学家厄拉多塞所发明的定理，它定义了任何给定的直角三角形，它的两个直角边的长度之和等于其斜边的长度平方。

最初的证明是分割型的。设a、b为直角三角形的直角边，c为斜边。考虑下图两个边长都是a+b的正方形A、B。将A分成六部分，将B分成五部分。

勾股定理的证明全过程

1、勾股定理：直角三角形中，两条直角边的平方和等于斜边的平方，即在以a、b为直角边，c为斜边的三角形中有a^2+b^2=c^2。

2、证法1 做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形这两个正方形的边长都是a+b，所以面积相等。

3、勾股定理证明方法如下：在欧几里得的《几何原本》一书中给出勾股定理的以下证明。设△ABC为一直角三角形，其中A为直角。从A点画一直线至对边，使其垂直于对边。

勾股定理是如何推导的?

勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理。

证明如下：已知一个正方形ABCD，边长为a＋b，正方形ABCD各边各取一个点O、P、E、G，构成一个四边形OPEG。已知，BO=AP=DE=CG=a，OA=PD=EC=GB=b。

最初的证明是分割型的。设a、b为直角三角形的直角边，c为斜边。考虑下图两个边长都是a+b的正方形A、B。将A分成六部分，将B分成五部分。

勾股定理是指在直角三角形中，两个直角边的平方和等于斜边的平方，如直角边分别为a、b，斜边为c，则一定有 c=a+b，如果a=3，b=4，则c=3+4=25，所以c=5，这就是“勾三股四弦五”。

勾股定理的证明是论证几何的发端。勾股定理是历史上第一个把数与形联系起来的定理，即它是第一个把几何与代数联系起来的定理。勾股定理导致了无理数的发现，引起第一次数学危机，大大加深了人们对数的理解。

到此，以上就是小编对于勾股定理推论过程是什么的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。