本篇目录:
sinx的导数怎么求啊?
1、(sinx)^3求导=3(sinx)^2*cosx,(sinx)^3的导数等于(u)^3u,其中u=sinx,得到(sinx)^3的导数等于3(sinx)^2*cosx,(sinx)^n求导=n(sinx)^(n-1)*cosx,(cosx)^n求导=-n(cosx)^(n-1)*sinx。
2、sinx的n阶导=sin(x+n兀/2),所以x等于零时,n阶导值为:sin(n兀/2)=0 ,n=2m,= (一1)^(m一1) n=2m一1。
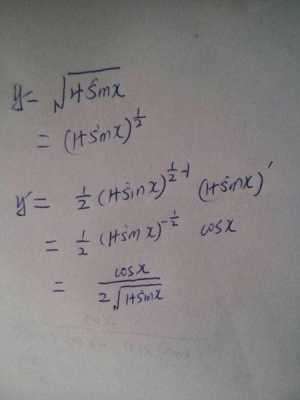
3、sinx=[e^(ix)-e^(-ix)]/(2i)。高等代数中三角函数的指数表示(由泰勒级数易得):sinx=[e^(ix)-e^(-ix)]/(2i) 。cosx=[e^(ix)+e^(-ix)]/2 。
4、对于函数 f(x) = sin(x),它的导数可以使用求导法则来计算。在这种情况下,我们可以使用链式法则来求出 sin(x) 的导数。根据链式法则,如果 f(x) = g(h(x)),那么 f(x) = g(h(x)) * h(x)。
求函数y=sinx的导数是多少,怎么推导
所以y=sinx 的导数为2cos(x+△x/2)*1/2,在△x趋向0时,导数为cosx。
sinx的导数是cosx(其中x为变量),sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
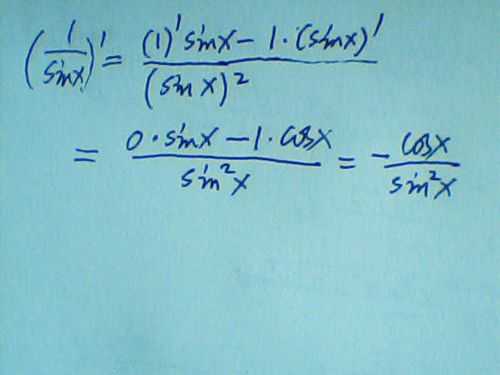
是sin(1/x)的话导数是[-cos(1/x)]/x^2,是1/sinx的话是-cosx/(sinx)^2。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是 -sinX,这是因为两个函数的不同的升降区间造成的。
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f(x0)或df(x0)/dx。
sinx的平方求导如下:先求外函数y=(sinx),再求内函数sinx的导数,即cosx。故(sinx)的导数为2sinxcos,也就是sin2x。
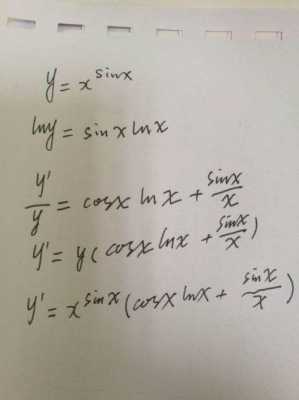
y=sinx求导,谢谢
1、sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是 -sinX,这是因为两个函数的不同的升降区间造成的。
2、- 常用函数的导数规则,如:f(x) = sin(x),f(x) = cos(x),f(x) = e^x,等等。以下是一个示例表格,展示常见函数的导数:请注意,这只是一份示例表格,实际上还有更多的函数和规则。
3、sin平方x的导数可以写成:(sinx)=2sinx(sinx)=2sinxcosx=sin2x。
4、sinX的导数是cosX,而cosX的导数是 -sinX。
求函数y=sinx的导数
1、sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是 -sinX,这是因为两个函数的不同的升降区间造成的。
2、是sin(1/x)的话导数是[-cos(1/x)]/x^2,是1/sinx的话是-cosx/(sinx)^2。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
3、sinx平方:y=sinx^2,y=cosx^2*2x=2xcosx^2 导数是函数图像在某一点处的斜率,也就是纵坐标增量(Δy)和横坐标增量(Δx)在Δx--0时的比值。
到此,以上就是小编对于的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏