随机过程数学期望（随机过程的数学期望是随机过程的什么平均）-义乌市趣迅电子商务商行

本篇目录：

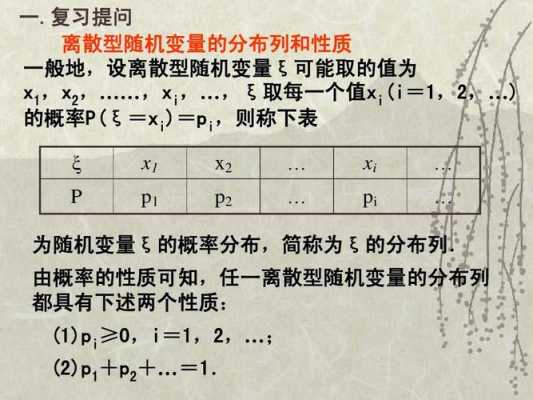
1、连续函数求期望的公式如下：E(X) = X1*p(X1）+ X2*p(X2）+……+ Xn*p(Xn) = X1*f1(X1）+ X2*f2(X2）+……+ Xn*fn(Xn)。X；1，X；2，X；3，……，X。

2、机变量服从二项分布数学期望等于np。随机变量服从二项分布可用公式E(X)=np，D(X)=np(1-p)计算期望和方差，如果随机变量只取得有限个值或无穷能按一定次序一—列出，其值域为一个或若干个有限或无限区间。

3、…p(Xn)、为X对应取值的概率，可理解为数据XXX3……Xn出现的频率高f(Xi)，则：连续型：设连续性随机变量X的概率密度函数为f(x)，若积分绝对收敛，则称积分的值为随机变量的数学期望，记为E(X)。

4、这个公式描述了随机变量 X 取值的加权平均，其中 xi 是随机变量 X 的第 i 个可能取值，pi 是相应的概率。如果随机变量 X 是一个连续型随机变量，其概率密度函数为 f(x)，那么数学期望 E[X] 的定义稍有不同。

5、数学期望公式是：E(X) = X1*p(X1） + X2*p(X2） + …… + Xn*p(Xn) = X1*f1(X1） + X2*f2(X2） + …… + Xn*fn(Xn)X ；1，X ；2，X ；3，……，X。

6、n为这离散型随机变量，p(X1），p(X2），p(X3），……p(Xn)为这几个数据的概率函数。

广义平均随机过程的数学期望、方差与时间无关，自相关函数只与时间间隔有关。

广义平稳随机过程的方差是常数。平稳随机过程的均值与时间无关，是一个常数。平稳随机过程的自相关函数只与计算时取的时间间隔有关。满足以上两点，就是广义平稳随机过程。

广义平稳概念：若一个随机过程的数学期望及方差与时间无关，而其相关函数仅与τ有关，则称这个随机过程为广义平稳随机过程。

方差是对随机变量离散程度的度量，表示随机变量与其数学期望之间的偏差平方的平均值。对于随机变量X，其方差Var(X)的计算公式为：Var(X) = E[ (X - E(X))^2 ]，其中E(X)为X的数学期望。

即若一个随机过程的数学期望及方差与时间无关，而其相关函数仅与有关，宽平稳随机过程（广义平稳）：且自相关函数只与有关，则称为宽平稳随机过程，或称广义平稳随机过程。

1、一般来说平稳过程源自稳定的物理现象，而非平稳过程源自不稳定的物理现象。严平稳就是随机过程的每一组联合分布函数对于取定的不同时间原点是时不变的。

2、数学期望和方差公式为：EX=npDX=np（1-p）、EX=1/PDX=p^2/q、DX=E（X）^2-（EX）^2。对于2项分布（例子：在n次试验中有K次成功，每次成功概率为P，它的分布列求数学期望和方差）有EX=npDX=np（1-p）。

3、在数学中，平稳随机过程或者严平稳随机过程又称狭义平稳过程。

到此，以上就是小编对于随机过程的数学期望是随机过程的什么平均的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。