投影矩阵推导过程（投影矩阵的推导）-义乌市趣迅电子商务商行

本篇目录：

如果(m*xk+b-yk)*(m*(xk+1)+b-yk)=0，那么容易知道该直线与(xk，yk)、(xk+1，yk)两点确定的直线相交，对其他三条边也是这样操作。接下来的问题时如何求解一条直线被一个正方形所截线段的长度。

首先在电脑中，打开Dev-c++软件，点击“新建源代码”，如下图所示。具体程序如下，如下图所示。此次的程序最终目的是求出3x3的整型矩阵对角线元素之和，所以要向计算机输入3x3矩阵中的所有元素。

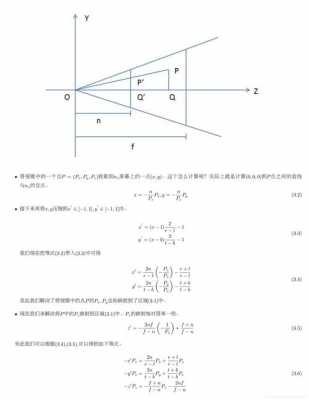
投影向量的计算公式：向量a·向量b=|a|*|b|*cosΘ。平面向量是在二维平面内既有方向又有大小的量，物理学中也称作矢量，与之相对的是只有大小、没有方向的数量。

定义一个名为array1的数组并赋值：double[，] array1 = new double[3， 3] { { 1， 2， 3 }， { 4， 5， 6 }， { 7， 8， 9 } }；下面求该矩阵转置矩阵。

1、投影矩阵的平方等于投影矩阵。这个结论可以通过投影矩阵的定义来证明。投影矩阵是指一个矩阵P，满足P^2=P，即对于任何向量v，P(Pv)=Pv。也就是说，将向量投影到P的列空间上，再次进行投影，结果不会改变。

2、矩阵的逆定义：设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=I。则我们称B是A的逆矩阵，而A则被称为可逆矩阵。

3、垂直投影矩阵的性质：投影矩阵不可逆，投影矩阵是一个对称矩阵。投影矩阵不可逆行列式的值为0，条件数无穷大，说明该矩阵不可逆是一个奇异矩阵singularmatrix。投影矩阵是一个对称矩阵最经典的对称矩阵就是单位矩阵Identitymatrix。

4、投影矩阵负责给我们的场景增加透视。 glLoadIdentity() 的功能是重置当前指定的矩阵为单位矩阵。在glLoadIdentity() 之后我们为场景设置了透视图。

5、这个矩阵是通用的视锥投影矩阵。如果说观察的是对称的话，即，上面的矩阵可以化简为：同样的我们也可以根据等式七求出的值在我们继续后面的内容之前，我们先仔细看看上面之间的关系。

2、m必在垂直于平面，含有p，q两点的面上。求出两平面的交线。这样就变成了同一平面上p，q和一条直线，求直线上点使得|pm|+|mq|最短的题目。pq在直线两边的话，直接就是pq连线。

3、在向量代数中，将向量b投影到向量a上的投影向量的公式可以使用向量点积（内积）来表示。

到此，以上就是小编对于投影矩阵的推导的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。