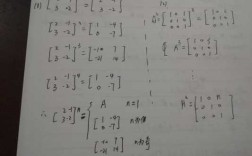本篇目录:
矩阵怎么对角化,求详细过程
矩阵对角化有三种方法 利用特征值和特征向量将矩阵对角化 由于这种方法相对来说比较基储简单、机械,一般教材都有详细介绍,这里用图示加以总结。
在矩阵对角化的过程中,我们需要求解的是矩阵A相似于对角矩阵D,即存在一个可逆矩阵P,使得PAP^-1 = D。在这个过程中,我们可以使用矩阵的初等变换来达到对角化的目的。

找到一个矩阵,我们对这个矩阵进行是否能够对角化的判断,我们暂且对把这个定义成A矩阵 我们需要用到一个公式,如下图所示,我们这一步就是直接按照公式套入就可以了。
如果存在可逆矩阵X使A相似与一个对角矩阵B,那么说A可对角化。相应的,如果线性变换a在基m下的矩阵为A,并且A相似于对角矩阵B,那么另X为过度矩阵即可求出基n,并且在n下线性变换a的矩阵为对角矩阵,从而达到了化简。
矩阵对角化问题求解
n阶矩阵A可对角化的 充分必要条件是: A有n个线性无关的特征向量。当矩阵A是实对称矩阵时,一定满足上述条件,即实对称矩阵必可对角化。
另外补充一点, 一般情况下题目要求都是求正交矩阵Q来对实对称阵对角化的,这样目的是想解决实际问题——二次型。

矩阵可对角化的充要条件是对于每个特征值αi,有αi的重数等于度数也就是说,比如矩阵A可以对角化,且有一个特征值a且a为5重根,则对于a必须有5个线性无关的特征向量。
矩阵对角化有三种方法 利用特征值和特征向量将矩阵对角化 由于这种方法相对来说比较基储简单、机械,一般教材都有详细介绍,这里用图示加以总结。
给定对称阵A,求正交阵U,使得U^TAU=U^(-1)AU=D是对角阵。一般而言U都不是惟一的,特别是A有重特征值时,答案更不是惟一的。但这没有关系,只要U的列向量是对应的特征向量,那就没有问题。
所有特征根都不相等,那么不用说,绝对可以对角化 有等根,只需要等根(也就是重特征值)对应的那几个特征向量是线性无关的,那么也可以对角化,如果不是,那么就不能了。

当x为何值时,矩阵能对角化,需要详细过程,谢谢?
矩阵对角化的条件和步骤是A2=A 可以x2-x=0看作A的一个零化多项式,再由无重根就可得到该矩阵可对角化。
一个特征值只能有一个特征向量,(非重根)又一个重根,那么有可能有两个线性无关的特征向量,也有可能没有两个线性无关的特征向量(只有一个)。不可能多于两个。
判断矩阵是否可对角化方法:先求特征值,如果没有相重的特征值,一定可对角化。
在这个过程中,A要能对角化有两点很重要:P是怎么构成的?P由n个线性无关的向量组成,并且向量来自A的特征向量空间。
可对角化矩阵和映射在线性代数中有重要价值,因为对角矩阵特别容易处理:它们的特征值和特征向量是已知的,并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。
复次数 可对角化矩阵和映射在线性代数中有重要价值,因为对角矩阵特别容易处理: 它们的特征值和特征向量是已知的,并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。
正交对角化步骤
1、将对称矩阵正交对角化的方法:求出对称矩阵A的特征值;由(AE )x= 0 ,求出矩阵A对应的特征的特征向量;将属于的特征向量施密特正交化;将所有特征向量单位化。
2、比如特征值为a,对应特征向量为A,当你把a写在对角矩阵第一列的时候,A就对应P的第一列。然后就是把P化成正交矩阵了。实对称矩阵有一个性质就是,当特征值不同时,特征向量必正交。
3、实对称矩阵一定可以找出一个正交矩阵,使实对称矩阵对角化。
4、这是一个对称矩阵,对称矩阵一定可以被对角化,也一定可以被正交矩阵对角化。对角化的一般方法是特征值特征向量法,其他还有初等变换法,配方法等等。
5、第一个问题:一般默认“相似对角化”可以简称“对角化”,而“合同对角化”就叫“合同对角化”。第二个问题:感觉你说的应该是”正交对角化“,指的是用正交矩阵进行相似对角化。
矩阵对角化
利用矩阵的初等变换将矩阵对角化 矩阵的初等变换 矩阵的初等行变换和初等列变换,统称矩阵的初等变换。
实对称矩阵一定能对角化 。不用厄米特矩阵,也不用二次型。若能证明下列命题,你的问题便也立即得到解决了。设A是一个n阶实对称矩阵,那么可以找到n阶正交矩阵T,使得(T的逆阵)AT为对角矩阵。
判断矩阵是否可对角化方法:先求特征值,如果没有相重的特征值,一定可对角化。
矩阵对角化的条件和步骤是A2=A 可以x2-x=0看作A的一个零化多项式,再由无重根就可得到该矩阵可对角化。
Jordan矩阵有一个重要的性质:它可以通过初等行变换转化为对角矩阵。这是一个非常重要的结论,在矩阵的理论和应用中都有着广泛的应用。
到此,以上就是小编对于对角化的本质的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏