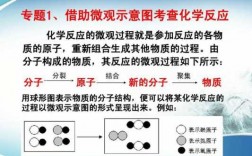
本篇目录:
- 1、梯形面积的推理过程
- 2、梯形的面积是怎么来的
- 3、梯形面积的推导过程是什么?
梯形面积的推理过程
梯形的面积=1/2ah+1/2bh=1/2(a+b)h 。推导四:一个梯形上底为a,下底为b,高为h。在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。(参见图四)则有:平行四边形的面积=ah 。
用平行四边形推导梯形面积的方法:先将两个相等的梯形拼成一个平行四边形,设梯形上底长为a,下底长为b。则平行四边形的底长为高设为h,先算出平行四边形的面积为:底高=(a+b)*h。
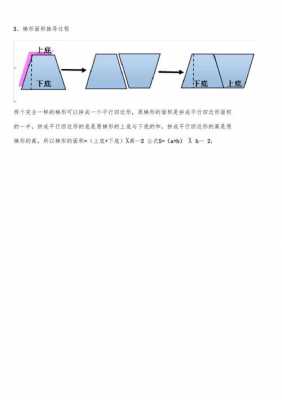
梯形的面积公式是由平行四边形来推导的,就是2个梯形一正一倒的和起来变成一个平行四边形,所以就得需要:上底加下底,高就还是梯形的高,但由于是2个梯形,所以就要除2。将两个完全一样的梯形拼成一个平行四边形。
梯形的面积公式:(上底+下底)×高÷2 梯形的面积等于上下两底之和与高的乘积的一半。如果梯形的上下两底分别用 a和 b表示,高用 h表示,梯形的面积s=(a+b)×h÷2 。
梯形的面积是怎么来的
1、梯形的面积=1/2ah+1/2bh=1/2(a+b)h 。推导四:一个梯形上底为a,下底为b,高为h。在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。(参见图四)则有:平行四边形的面积=ah 。
2、你的两个括号,说明了,我们只需要在梯形里面添一条对角线,就形成了两个三角形,一个是以上底为底边,另一个以下底为底边。所以梯形的面积公式,就等于两个三角形的面积公式之和。

3、梯形面积公式 梯形的面积公式:(上底+下底)×高÷2 梯形的面积等于上下两底之和与高的乘积的一半。如果梯形的上下两底分别用 a和 b表示,高用 h表示,梯形的面积s=(a+b)×h÷2 。
4、②梯形的面积公式:中位线×高,用字母表示:L·h。③对角线互相垂直的梯形面积为:对角线×对角线÷2。梯形平行的两边叫做梯形的底边,较长的一条底边叫下底,较短的一条底边叫上底。
5、梯形面积公式:S=1/2(上底+下底)*高 判定 两腰相等的梯形是等腰梯形;同一底上的两个角相等的梯形是等腰梯形;对角线相等的梯形是等腰梯形。
6、梯形的面积等于上下两底之和与高的乘积的一半。如果梯形的上下两底分别用 a和 b表示,高用 h表示,梯形的面积s=(a+b)×h÷2 。
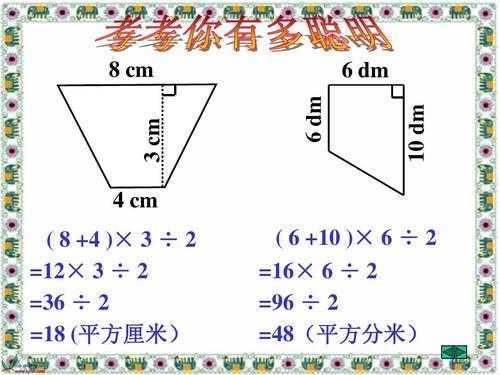
梯形面积的推导过程是什么?
梯形的面积推导过程可以用拼组法、分割法、割补法等方法进行推导。拼组法(1):用两个完全一样的梯形,调整方向后拼成一个平行四边形。平行四边形的底=梯形的上底+下底,高=梯形的高,面积=底×高。
梯形面积推导方法7种分别为:利用平行四边形的面积公式推导、利用三角形的面积公式推导、利用长方形的面积公式推导、利用两个三角形的面积公式推导、利用组合图形推导等等。
梯形的面积公式是由平行四边形来推导的,就是2个梯形一正一倒的和起来变成一个平行四边形,所以就得需要:上底加下底,高就还是梯形的高,但由于是2个梯形,所以就要除2。将两个完全一样的梯形拼成一个平行四边形。
梯形面积公式推导过程如下:用平行四边形推导梯形面积的方法:先将两个相等的梯形拼成一个平行四边形,设梯形上底长为a,下底长为b。则平行四边形的底长为高设为h,先算出平行四边形的面积为:底*高=(a+b)*h。
到此,以上就是小编对于梯形面积变化规律的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏