本篇目录:
数字信号处理,关于Z变换的问题
很明显, 如果n0 ,对某个序列进行Z变换, Z^(-n),此时n为负数, -n就是正数。
零极点与高低通之间不能说是有明显的关系,而是一般我们通过适当的方式得出系统的频率响应,再根据系统稳定性的要求(这个与零极点有关),最终去推出系统的高低通特性。

在Z变换里,零点的位置表示系统的“谷”,极点的位置表示系统的“峰”,我们把有峰的地方看做信号可以通过的地方,而有谷的地方看做信号被截止的地方。
Z变换(Z-transformation)是对离散序列进行的一种数学变换,常用于求线性时不变差分方程的解。它在离散系统中的地位如同拉普拉斯变换在连续系统中的地位。
字母k的z变换等于多少
1、z变换的基本公式是a \cdot x[n] + b \cdot y[n] \stackrel{Z}{\longrightarrow} a \cdot X(z) + b \cdot Y(z)。位移定理。
2、即两序列褶积的z变换,等于两个序列的z变换的乘积。[例5]已知a(k)={a(0),a(1),a(2),a(3),a(4)}={1,1,1,1,1},且b(k)=a(k),求 褶积值y(k)=a(k)*b(k)。

3、对于任意一个右边序列a(k),其Z变换A(z)的收敛域位于一个以原点为圆心,以某个数值R为半径的圆的圆外。又知道,收敛域内不会有极点,所以R就等于A(z)的极点中离原点最远的那个极点到原点的距离。
拉氏变换如何转化为Z变换?
拉普拉斯逆变换是已知F(s) 求解 f(t) 的过程。用符号 表示。
Z变换可以把离散卷积变成多项式乘法,对离散数字系统能发挥很好的作用。
Z变换它的极径=1,也就是单位圆周上的变换,本质上就还是傅里叶变换,Z与拉普拉斯的关系自然就是Z=e^st。总结如下:fourier变换是将连续的时间域信号转变到频率域;它可以说是laplace变换的特例。
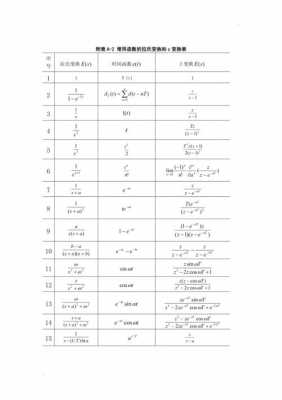
拉氏变换就是拉普拉斯变换,首先,傅里叶变换、拉普拉斯变换、z变换都是积分变换,拉普拉斯变换与z变换两种变换都是可逆的 ,分为正变化和逆变换。
n^2的Z变换怎么求,请写出详细过程及其
1、z变换的基本公式是a \cdot x[n] + b \cdot y[n] \stackrel{Z}{\longrightarrow} a \cdot X(z) + b \cdot Y(z)。位移定理。
2、离散时间序列 x(n) 的Z变换定义为X(z)=Σx(n)z-n ,式中z=e,σ为实变数,ω为实变量,j=,所以z是一个幅度为eб,相位为ω的复变量。x(n)和X(z)构成一个Z变换时 。
3、y(n-2)的z变换公式:z-1+z-1+z-n=p(z)p(z)*z-1=nz-(n+1)的级数,其正是q(z)=z-n的导数。q(z)=z-n的级数易求得z-1/1-z-1。求导得:z-2/(1-z-1)2。
到此,以上就是小编对于z变换的z的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏